If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.

Let a be the side of the square.

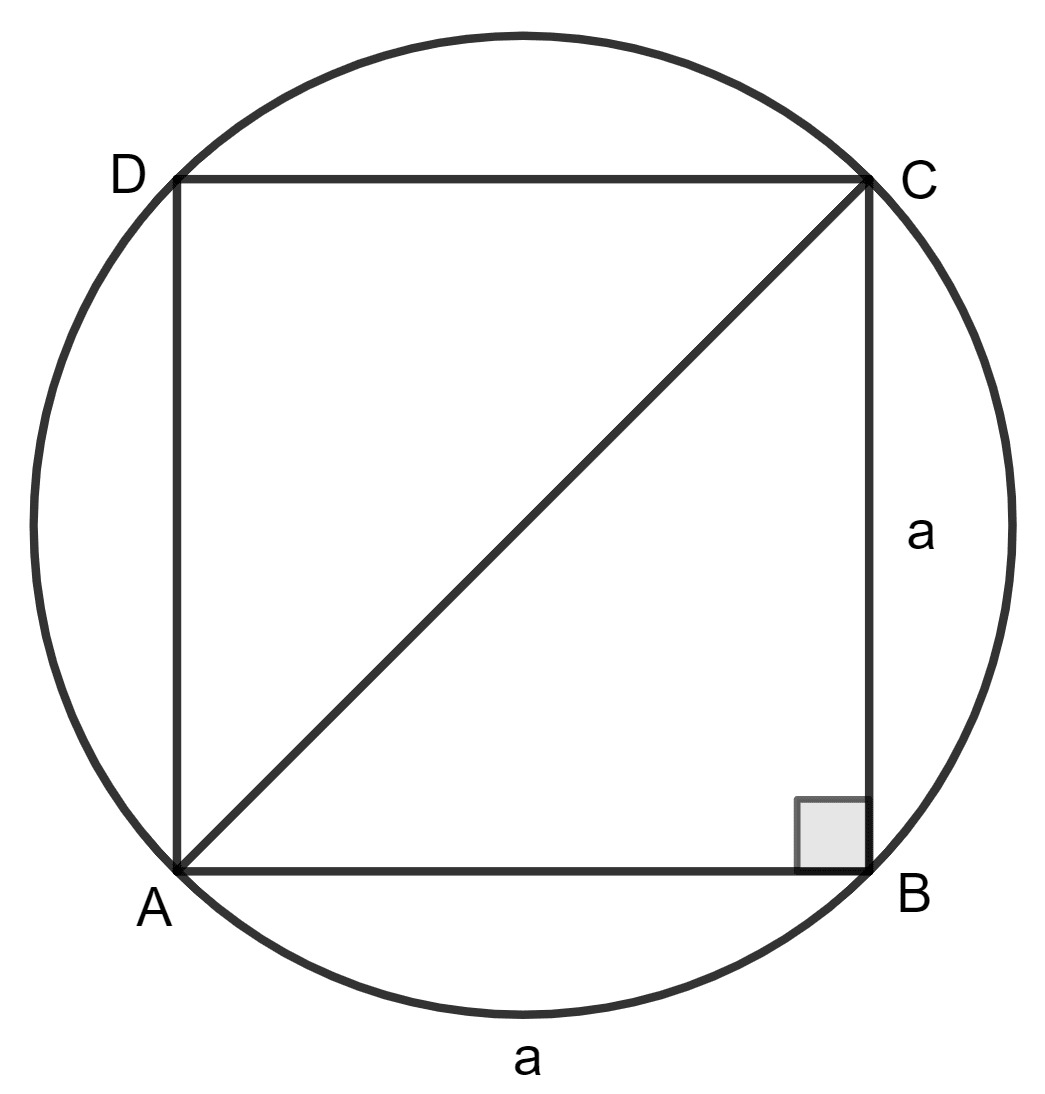
By using the Pythagoras theorem,

AB² + BC² = AC²

⇒ a² + a² = AC²

⇒ AC² = 2a²

⇒ AC = a $\sqrt{2}$

Diagonal of the square = Diameter of the circle

d = a $\sqrt{2}$

Radius, r = $\dfrac{d}{2}$ = $\dfrac{a \sqrt{2}}{2}$

Now, the ratio of the area of the circle to the area of the square is:

$= \dfrac{\text{Area of circle}}{\text{Area of square}}\\[1em] = \dfrac{πr^2}{\text{side}^2}\\[1em] = \dfrac{π \times \Big(\dfrac{a \sqrt{2}}{2}\Big)^2}{a^2}\\[1em] = \dfrac{π \times a^2 \times 2}{4a^2}\\[1em] = \dfrac{π \times a^2}{2a^2}\\[1em] = \dfrac{π}{2}\\[1em] = \dfrac{22}{14}\\[1em] = \dfrac{11}{7}\\[1em]$

Hence, the ratio of the area of the circle to the area of the square is 11 : 7.