If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.

Let AB and CD be the two equal chords (AB = CD = a). Let the chords intersect at point P. Join OP.

Draw OM and ON perpendicular to chords AB and CD respectively.

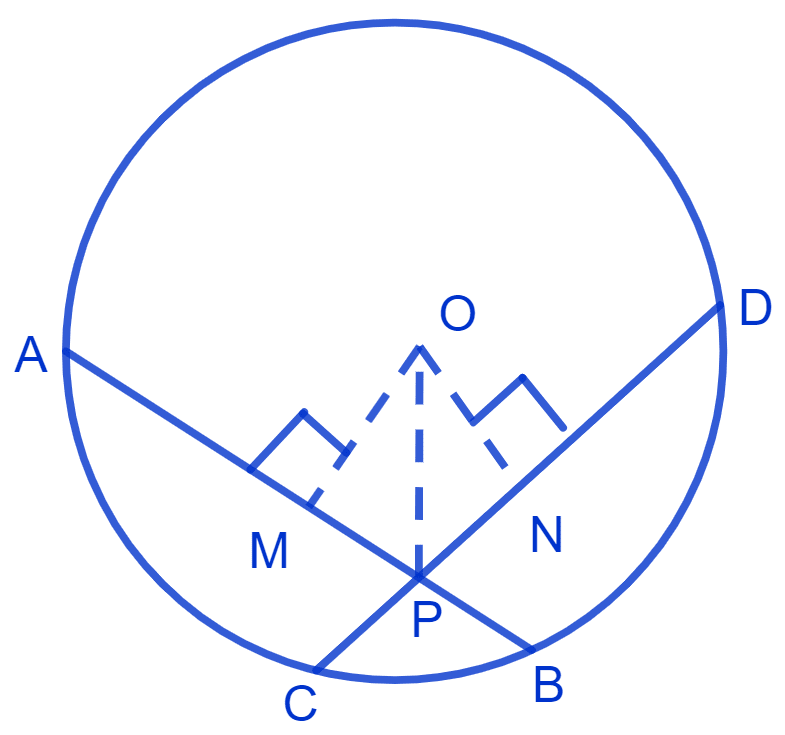
We know that,

Perpendicular from center bisects the chord.

∴ AM = MB = $\dfrac{AB}{2}$ and CN = DN = $\dfrac{CD}{2}$

Since, AB = CD.

∴ AM = MB = CN = DN = x(let) …..(1)

In ∆ OMP and ∆ ONP,

⇒ ∠M = ∠N (Both equal to 90°)

⇒ OP = OP (Common side)

⇒ OM = ON (Equal chords are equidistant from the center.)

∴ ∆ OMP ≅ ∆ ONP (By R.H.S congruence rule)

We know that,

Corresponding parts of congruent triangles are equal.

∴ MP = NP = y(let) (By C.P.C.T.) …..(2)

From figure,

⇒ CP = CN - NP = x - y and PB = MB - MP = x - y

∴ CP = PB.

From figure,

DP = CD - CP = a - (x - y) and AP = AB - BP = a - (x - y)

∴ AP = PD.

Hence, proved that if two equal chords of a circle intersect within the circle, the segments of one chord are equal to corresponding segments of the other chord.