The below image is that of a Digital Single Lense Reflector (DSLR) Camera which are used to take high resolution photographs by professional photographers. The second image of the below two is a schematic diagram of how an image is formed on the sensor of the camera. Based on your understanding of the lenses, answer the following questions.

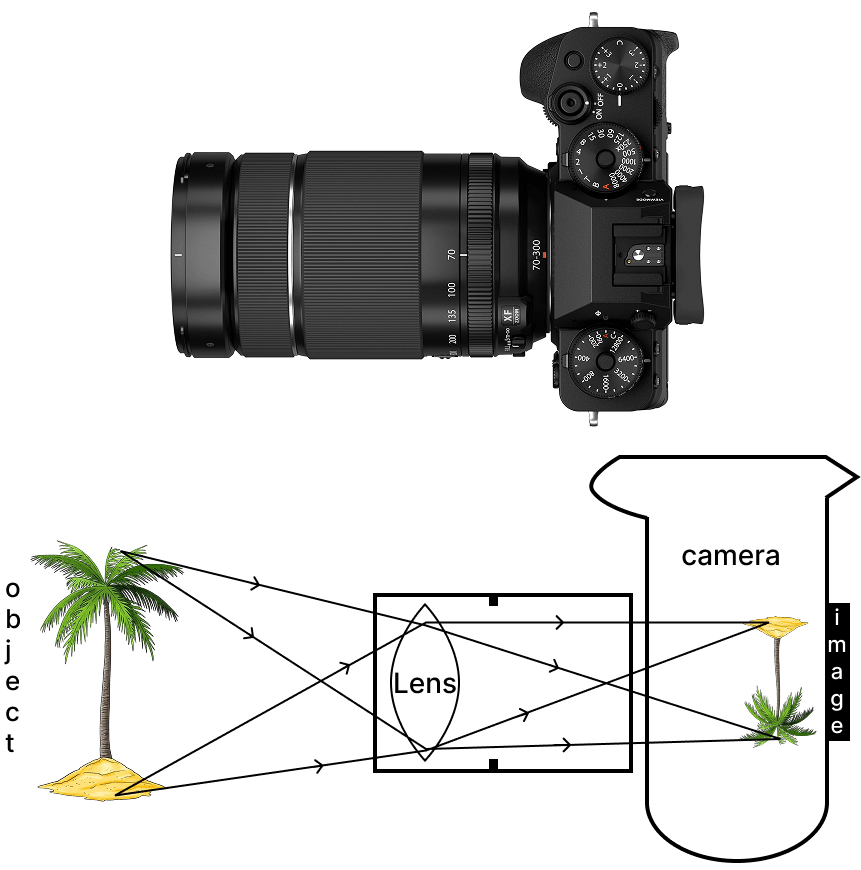
(a) What type of lens is used in the DSLR camera shown in the image?

(b) What type of image is formed on the sensor?

Attempt either subpart C or D.

(c) A photographer is using a DSLR camera with a lens of focal length f = 50 mm to take a close-up photograph of a small object. The lens projects an image onto the camera sensor that is located 60 mm behind the lens. Calculate the object distance (i.e., the distance between the object and the lens).

OR

(d) A photographer is using a DSLR camera to take a picture of a flower. The flower is positioned 150 mm away from the camera lens. The actual height of the flower is 80 mm, and the image height formed on the camera’s sensor is measured to be 20 mm. Calculate the focal length of the camera lens.

(a) Convex Lens.

(b) Real and Inverted.

(c) Given,

• Focal length of the lens ($\text f$) = 50 mm
• Image distance ($\text v$) = 60 mm

Let, object distance be '$\text u$'

By using the lens formula,

$\dfrac{1}{\text f} = \dfrac{1}{\text v} - \dfrac{1}{\text u} \\[1em] \Rightarrow \dfrac{1}{\text u} = \dfrac{1}{\text v} - \dfrac{1}{\text f} \\[1em] \Rightarrow \dfrac{1}{\text u} = \dfrac{1}{60} - \dfrac{1}{50} \\[1em] \Rightarrow \dfrac{1}{\text u} = \dfrac{5 - 6}{300} \\[1em] \Rightarrow \dfrac{1}{\text u} = -\dfrac{1}{300} \\[1em] \Rightarrow \text u = -300 \text { mm}$

Thus, the negative sign indicates that the object is located 300 mm in front of the lens (on the opposite side from the image).

(d) Given,

• Object distance ($\text u$) = -150 mm
• Actual height of the flower ($\text O$) = 80 mm
• Image height of the flower ($\text I$) = -20 mm

Here, negative sign indicates that the object is in front of the lens and the image is inverted.

As, magnification ($\text m$) of a lens is given by,

$\text m = \dfrac{\text I}{\text O} \\[1em] = -\dfrac{20}{80} \\[1em] = -\dfrac{1}{4} \\[1em]$

Let, image distance be '$\text v$'.

Then,

$\text m = \dfrac{\text v}{\text u} \\[1em] \Rightarrow \text v = \text m\text u \\[1em] = -\dfrac{1}{4} \times (-150) \\[1em] \Rightarrow \text v = 37.5\ \text {mm}$

Let, focal length of the lens be '$\text f$'.

Then, by using the lens formula,

$\dfrac{1}{\text f} = \dfrac{1}{\text v} - \dfrac{1}{\text u} \\[1em] \Rightarrow \dfrac{1}{\text f} = \dfrac{1}{37.5} - \dfrac{1}{(-150)} \\[1em] \Rightarrow \dfrac{1}{\text f} = \dfrac{4}{150} + \dfrac{1}{150} \\[1em] \Rightarrow \dfrac{1}{\text f} = \dfrac{4 + 1}{150} \\[1em] \Rightarrow \dfrac{1}{\text f} = \dfrac{5}{150} \\[1em] \Rightarrow \dfrac{1}{\text f} = \dfrac{1}{30} \\[1em] \Rightarrow \text f = 30 \text { mm}$

Hence, the focal length of the camera lens is 30 mm.