Mathematics
In a trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that :
AB + DC = 2EF.
Mid-point Theorem
9 Likes
Answer
Join BE and produce to meet CD produced at point P.
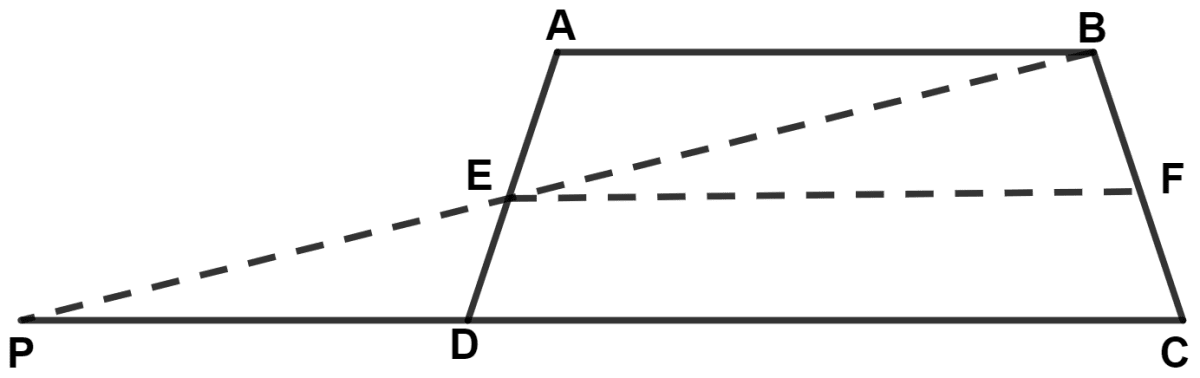
In △ PDE and △ BAE,
⇒ ∠PED = ∠BEF (Vertically opposite angles are equal)
⇒ AE = ED (Since, E is the mid-point of AD)
⇒ ∠EDP = ∠EAB (Alternate angles are equal)
∴ △ PDE ≅ △ BAE (By A.S.A. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
∴ BE = EP and AB = PD.
In △ BPC,
Since, E and F are mid-points of sides BP and BC respectively.
∴ EF = .
To prove :
AB + CD = 2EF ……..(1)
Substituting value in L.H.S. of equation (1), we get :
⇒ AB + CD = PD + CD = PC.
Substituting value in R.H.S. of equation (2), we get :
⇒ 2EF = = PC.
Since, L.H.S. = R.H.S.
Hence, proved that AB + CD = 2EF.
Answered By
2 Likes
Related Questions
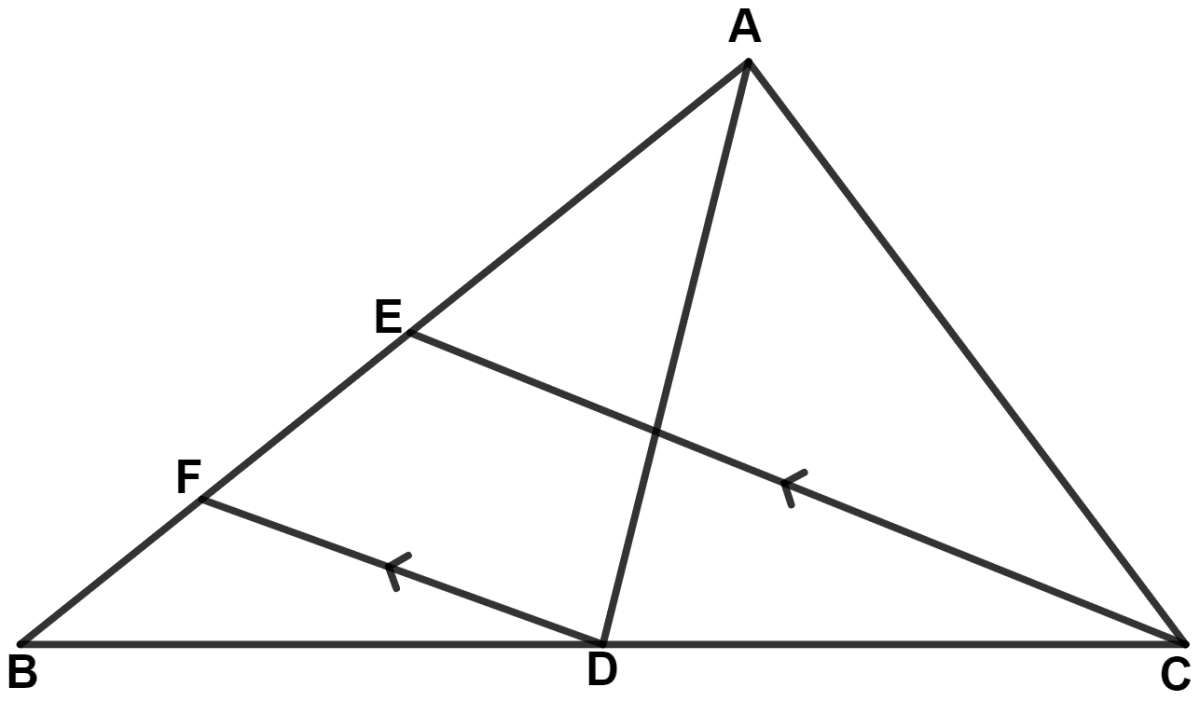
In the given figure, AD and CE are medians and DF // CE. Prove that : FB = .
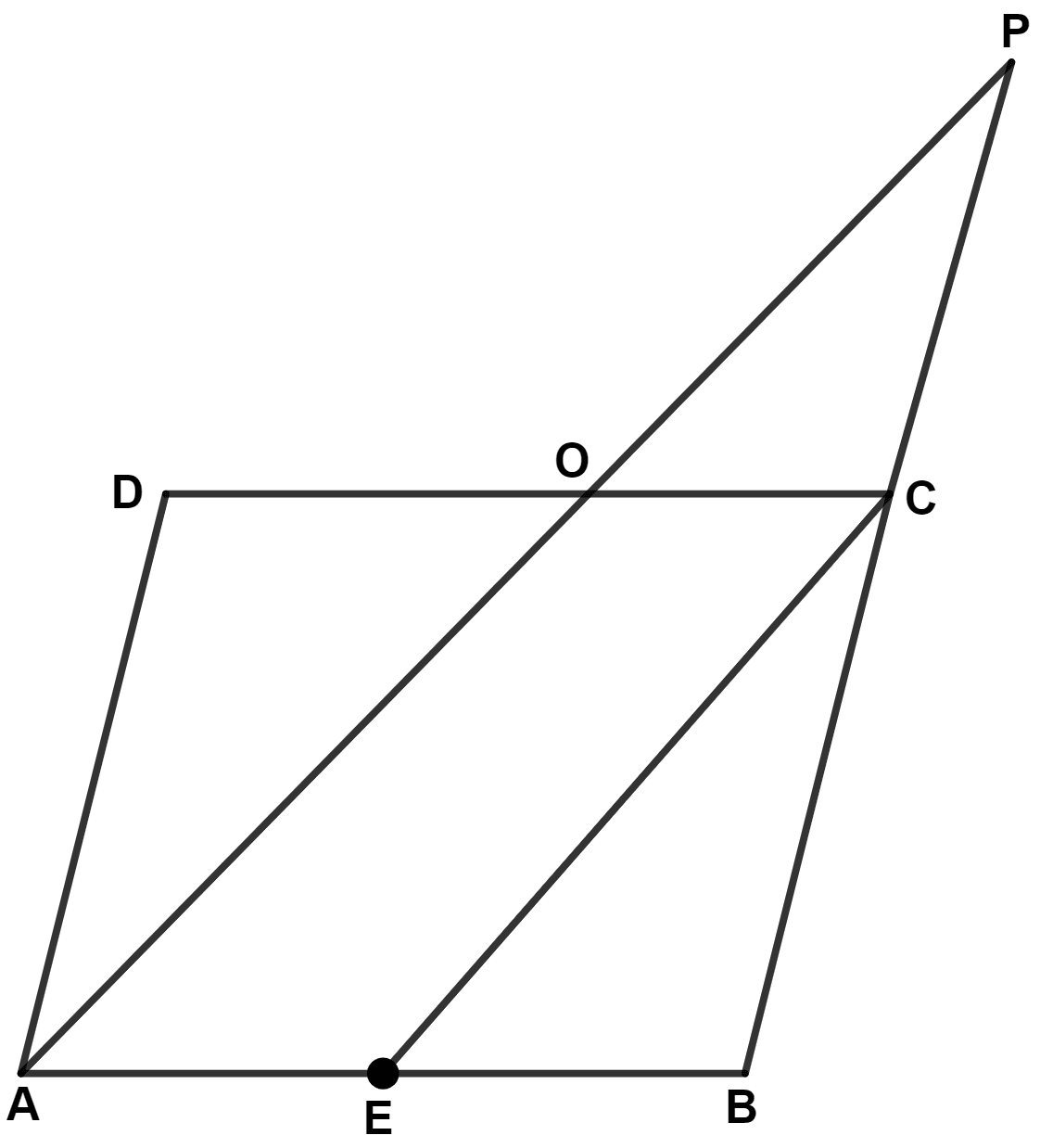
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
(i) BP = 2AD
(ii) O is mid-point of AP.
In △ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
Adjacent sides of a parallelogram are equal and one of diagonals is equal to any one of the sides of this parallelogram. Show that its diagonals are in the ratio .