Mathematics
In a triangle ABC, D is mid-point of BC; AD is produced upto E, so that DE = AD. Prove that :
(i) △ ABD and △ ECD are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
Answer
△ ABC with AD produced upto E is shown in the figure below:
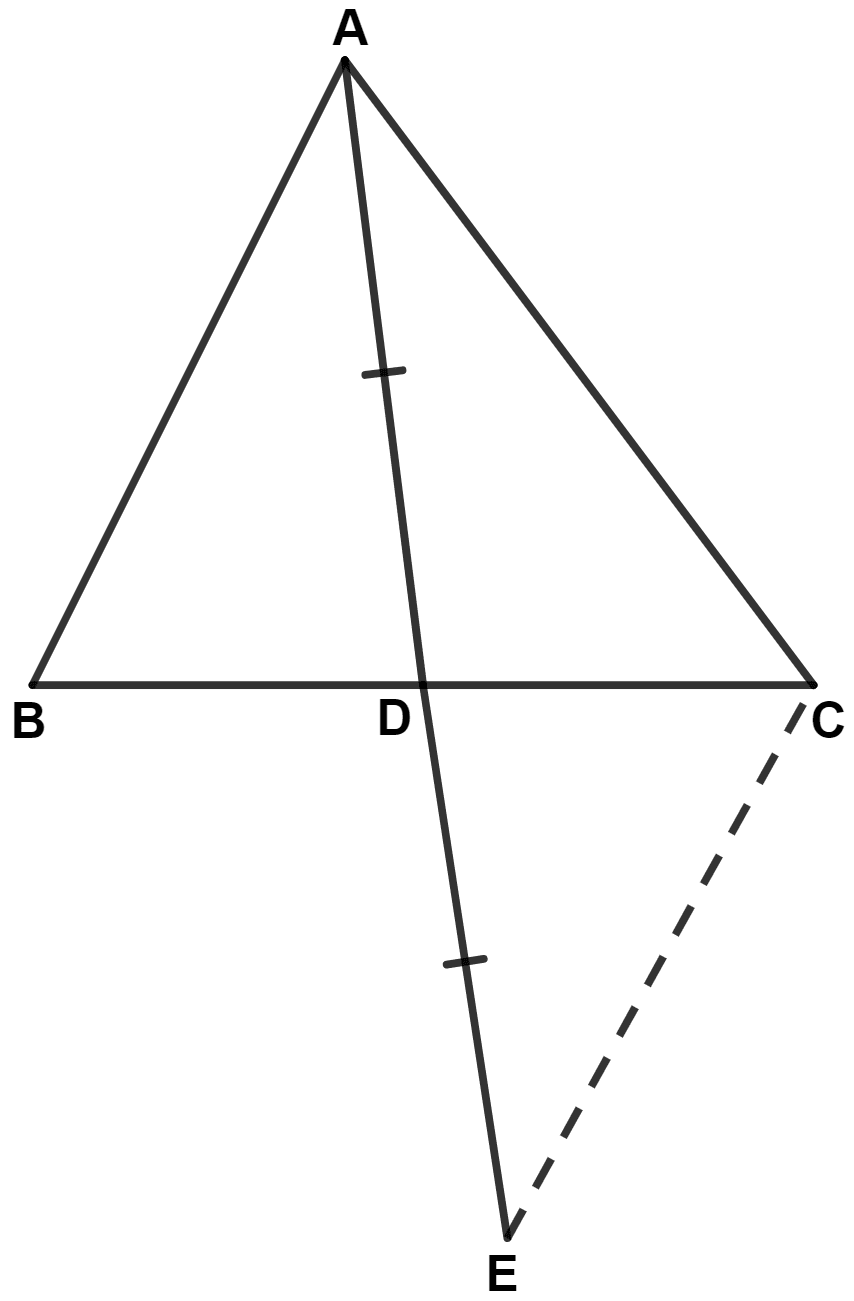
(i) In △ ABD and △ ECD,
⇒ AD = DE (Given)
⇒ BD = DC (As D is the mid-point of BC)
⇒ ∠ADB = ∠CDE (Vertically opposite angles are equal)
∴ △ ABD ≅ △ ECD (By S.A.S. axiom)
Hence, proved that △ ABD ≅ △ ECD.
(ii) Since,
△ ABD ≅ △ ECD (Proved above)
We know that,
Corresponding parts of congruent triangles are equal.
∴ AB = EC.
Hence, proved that AB = EC.
(iii) From figure,
∠ABD = ∠DCE (By C.P.C.T.C.)
Since, these are alternate angles and are also equal,
thus, it can be said, AB and EC are parallel with AE as transversal.
Hence, proved that AB is parallel to EC.
Related Questions
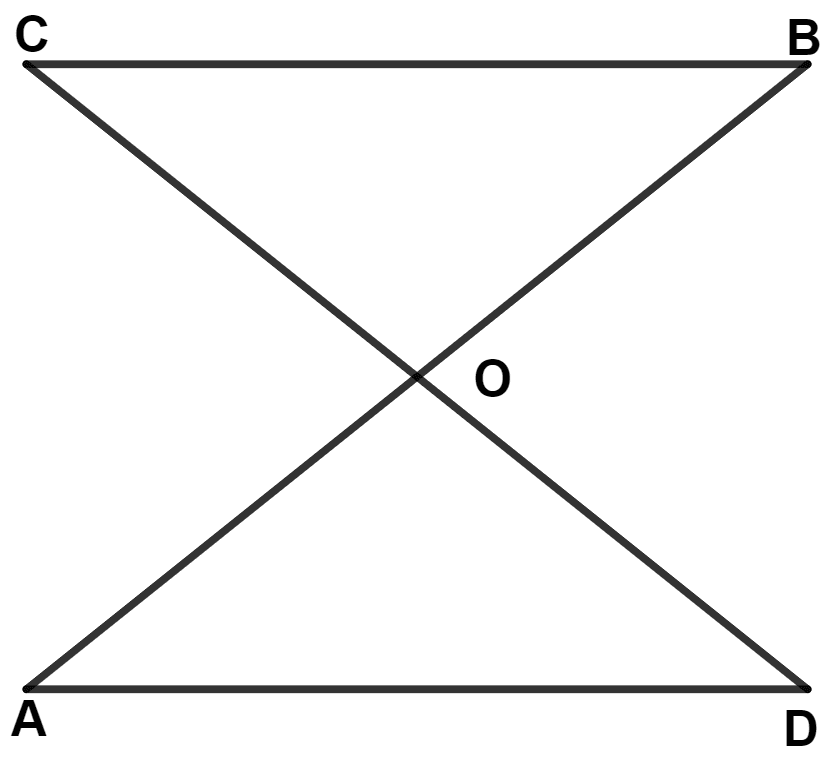
In the given figure, BC // DA and BC = DA, then :
AB and CD bisect each other
AB ≠ CD
OA = OC
OA = OD
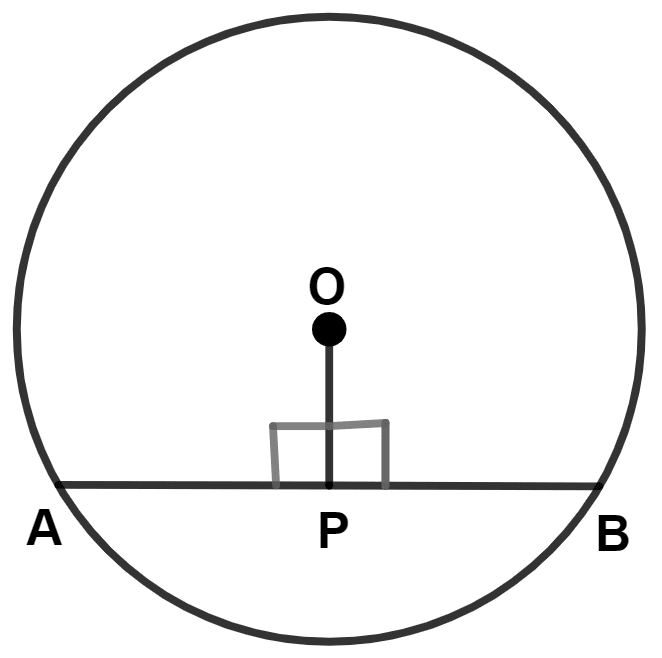
The following figure shows a circle with center O. If OP is perpendicular to AB, prove that AP = BP.
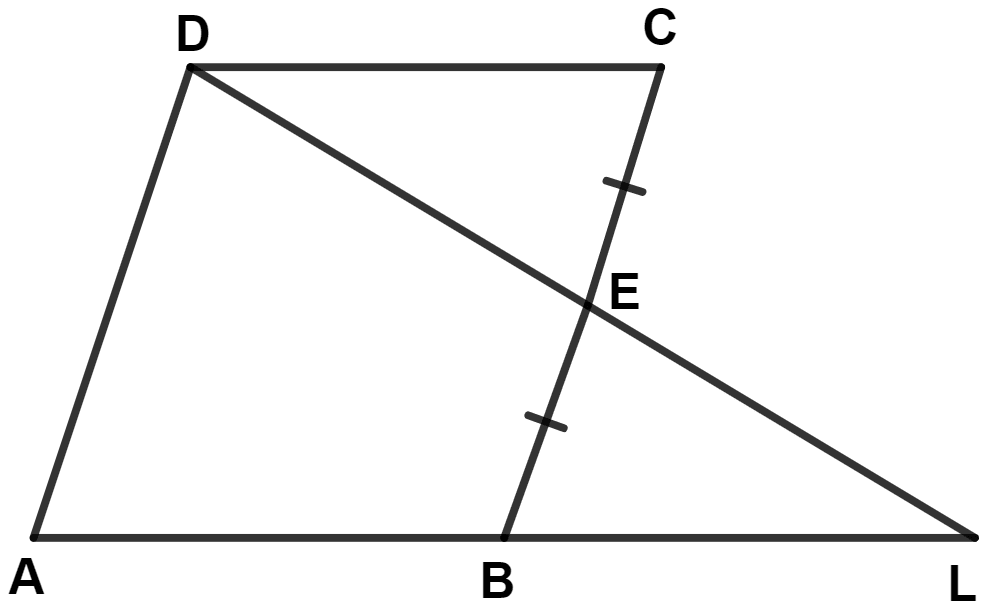
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid point of BC.
Prove that :
(i) △ DCE ≅ △ LBE
(ii) AB = BL
(iii) AL = 2DC
On the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) ∠CAD = ∠BAE
(ii) CD = BE.