Mathematics
In a triangle PQR; QR = PR and ∠P = 36°. Which is the largest side of the triangle ?
Answer
In △ PQR,
⇒ PR = QR (Given)
⇒ ∠Q = ∠P = 36°
By angle sum property of triangle,
⇒ ∠Q + ∠P + ∠R = 180°
⇒ 36° + 36° + ∠R = 180°
⇒ 72° + ∠R = 180°
⇒ ∠R = 180° - 72° = 108°.
Since, ∠R is greatest angle.
∴ PQ is the largest side. (In a triangle, side opposite to greatest angle is largest.)
Hence, PQ is the largest side.
Related Questions
In a quadrilateral ABCD,
AB + BC + CD + DA > AC + BD
AB + BC + CD + DA < AC + BD
AB + BC + CD + DA = AC + BD
AB + BC < AC
From the following figure, prove that : AB > CD.
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
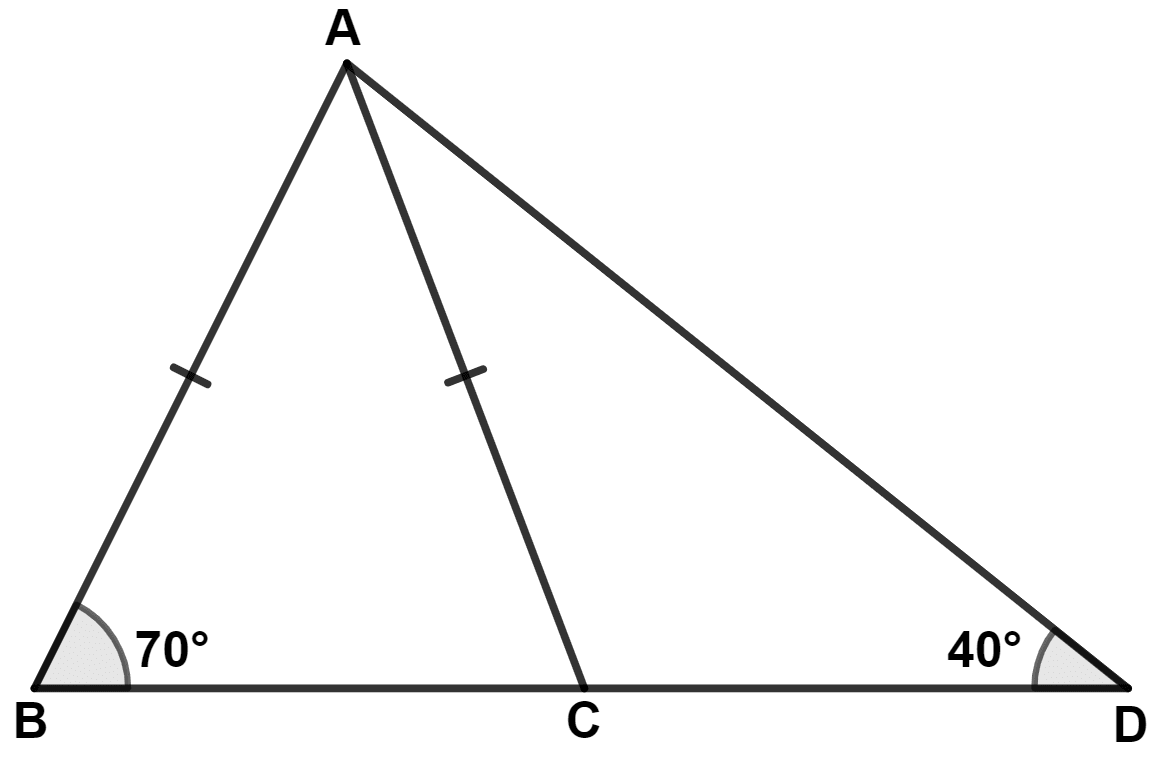
In each of the following figures, write BC, AC and CD in ascending order of their lengths.