Mathematics
In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:
Similarity
48 Likes
Answer
ΔABC is shown in the figure below:
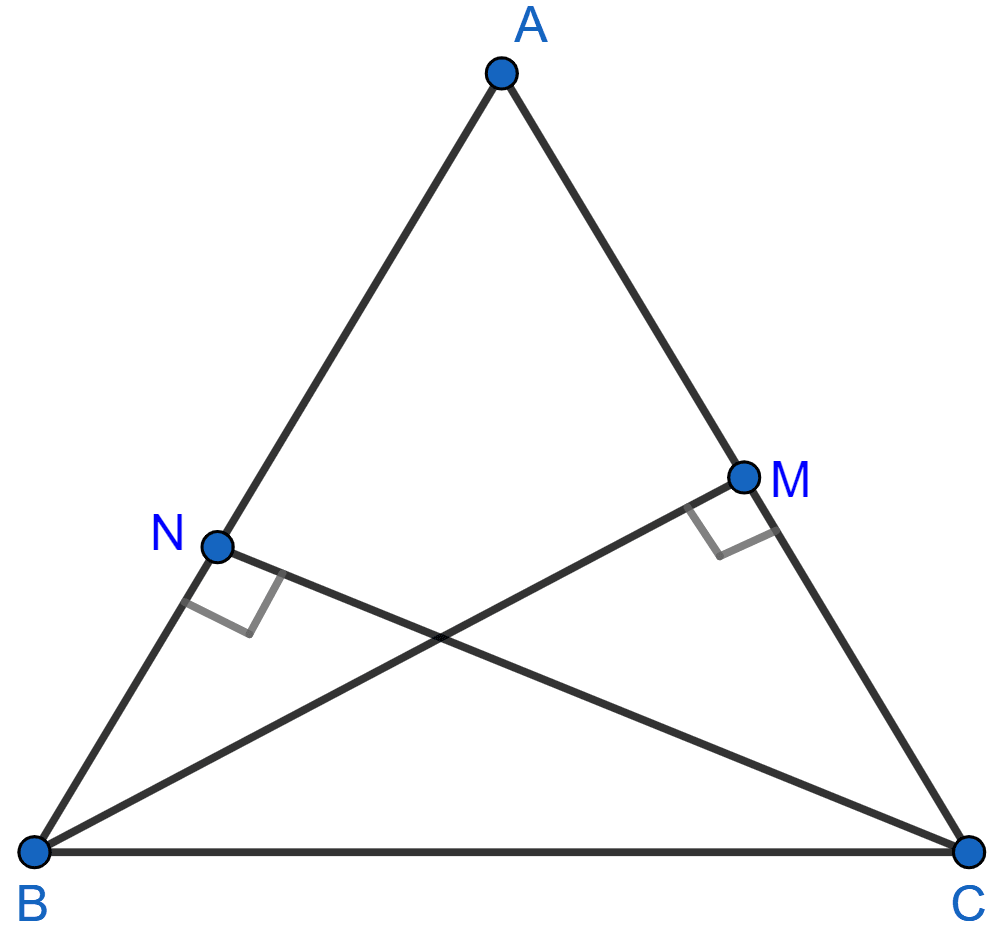
In ΔABM and ΔACN,
∠AMB = ∠ANC [Since, BM ⊥ AC and CN ⊥ AB]
∠BAM = ∠CAN [Common angle]
∴ ∆ABM ~ ∆ACN [By A.A.]
Since corresponding sides of similar triangles are proportional we have,
⇒
Hence, proved that .
Answered By
36 Likes
Related Questions
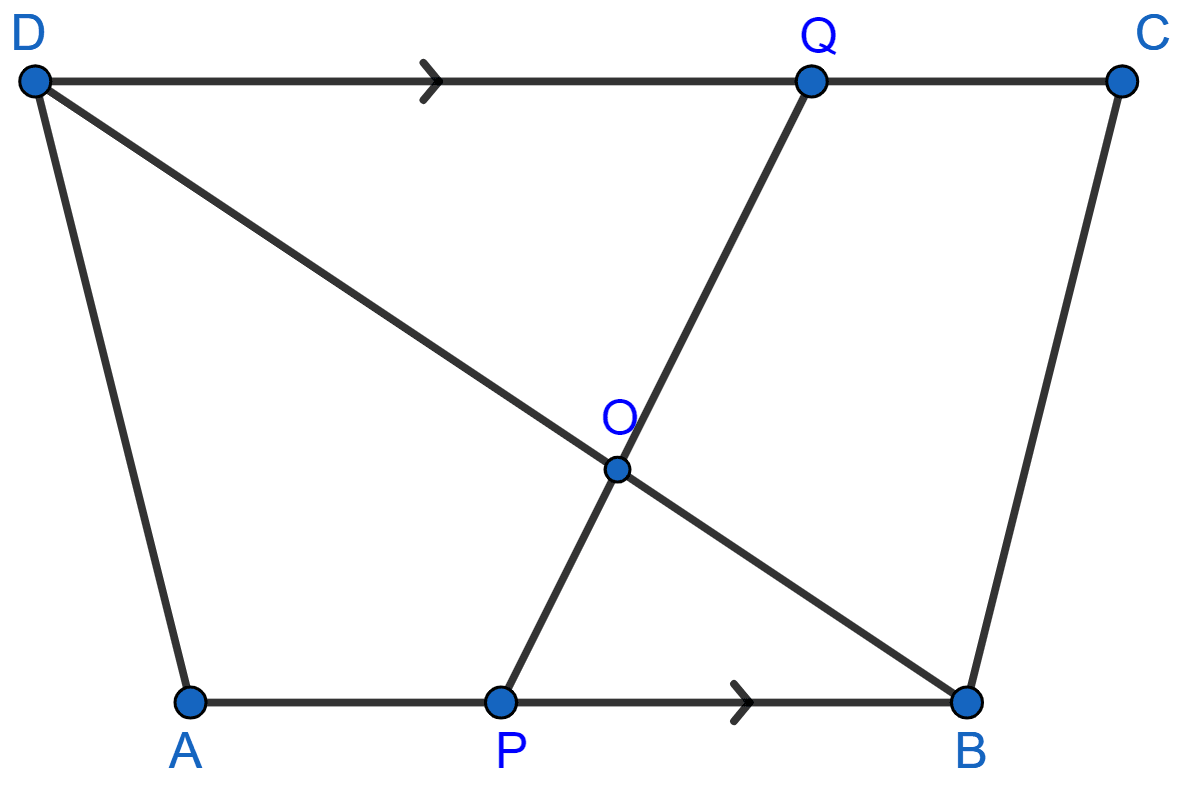
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that:
(i) ∆APC and ∆BPD are similar.
(ii) If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.

In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.
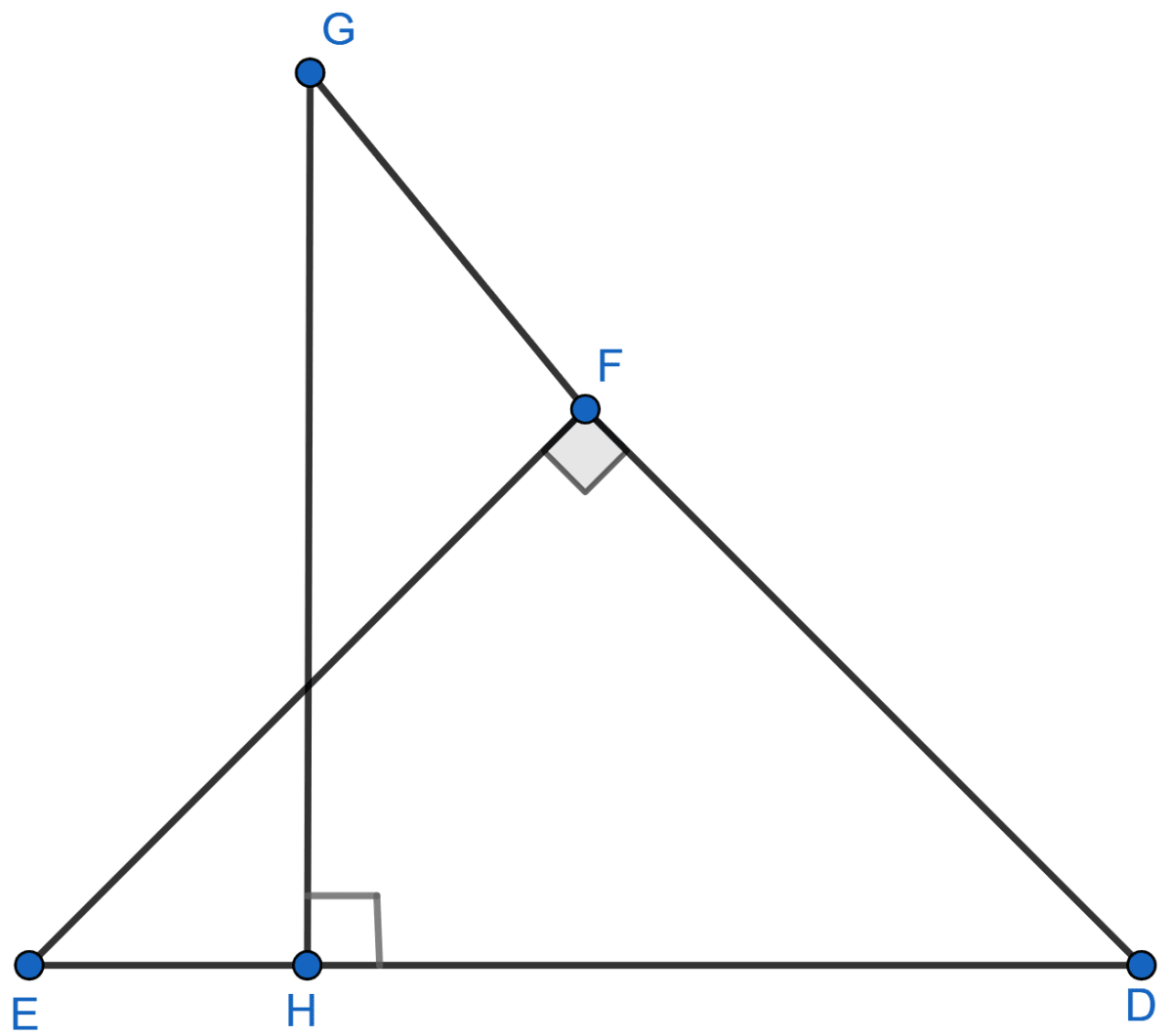
Given: ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x – 1 and DE = 4x + 2.
Find: the lengths of segments DG and DE.
In △PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that :
(i) PQ2 = PM × PR
(ii) QR2 = PR × MR
(iii) PQ2 + QR2 = PR2