Mathematics
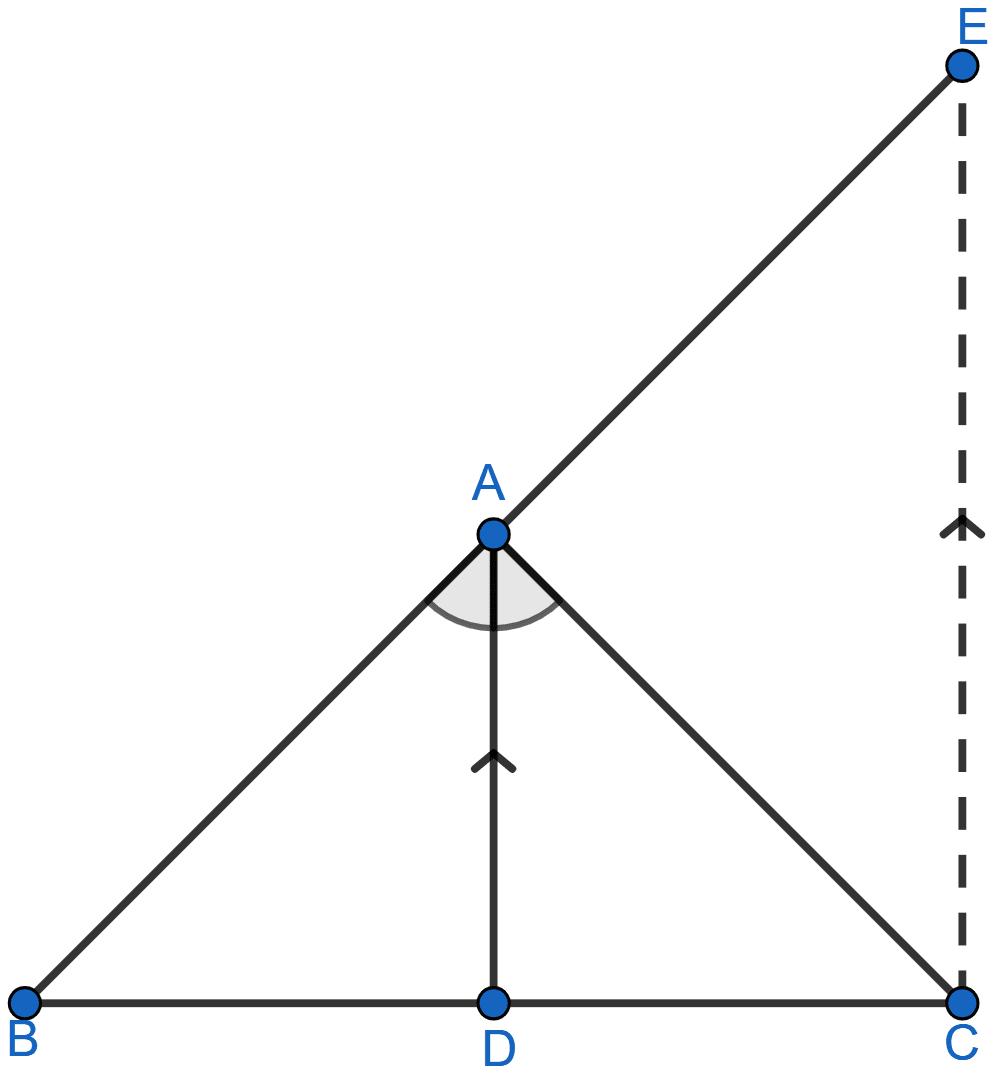
In △ABC, D is a point on BC such that AD is the bisector of ∠BAC. CE is drawn parallel to DA to meet BD produced at E. Prove that △CAE is isosceles.
Related Questions
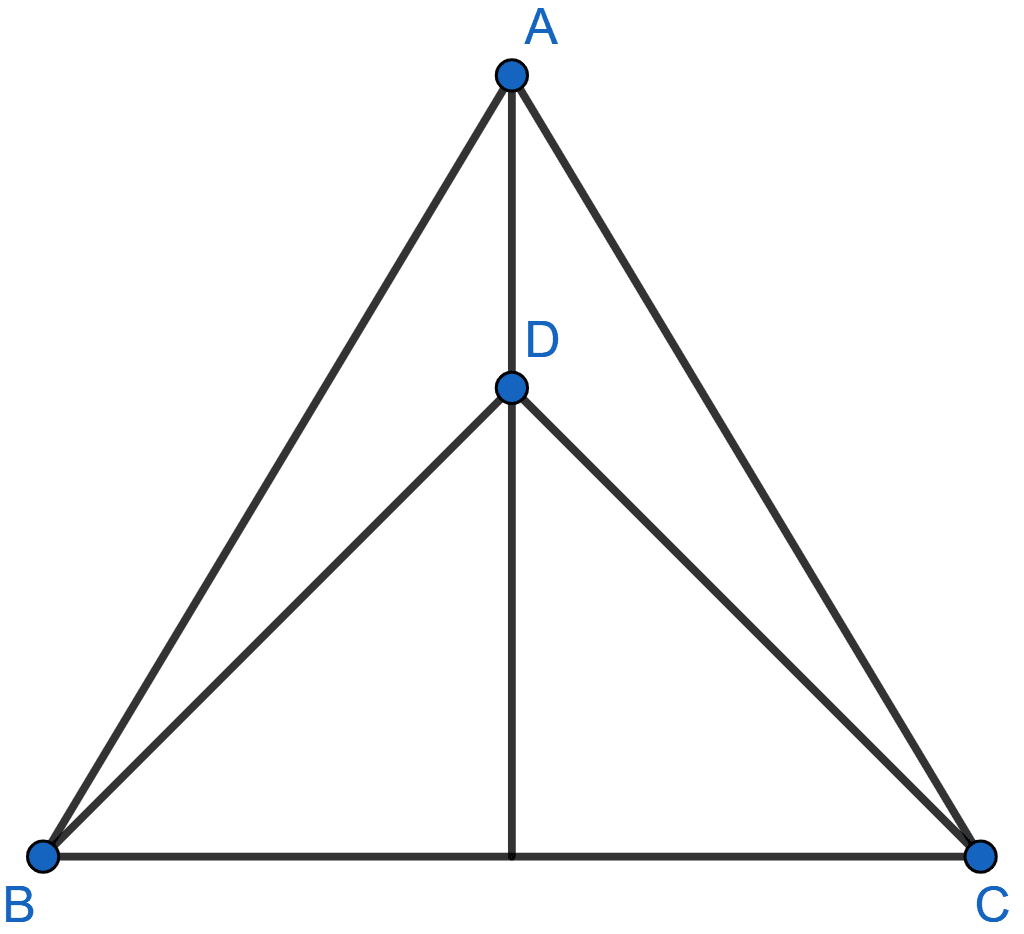
In the adjoining figure, AB = AC, D is a point in the interior of △ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of △ABC.
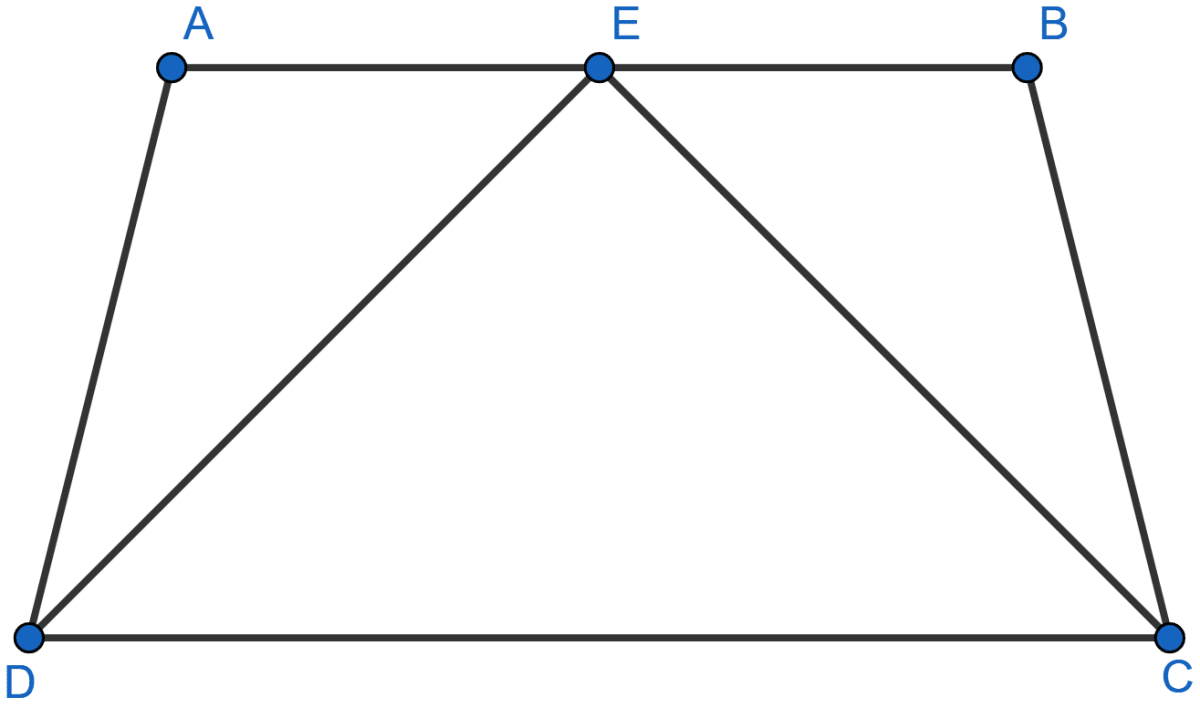
In the adjoining figure, AB || DC. CE and DE bisects ∠BCD and ∠ADC respectively. Prove that AB = AD + BC.
In the adjoining figure, ABC is a right angled triangle at B. ADEC and BCFG are squares. Prove that AF = BE.

In the adjoining figure, TR = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that RB = SA.