Mathematics
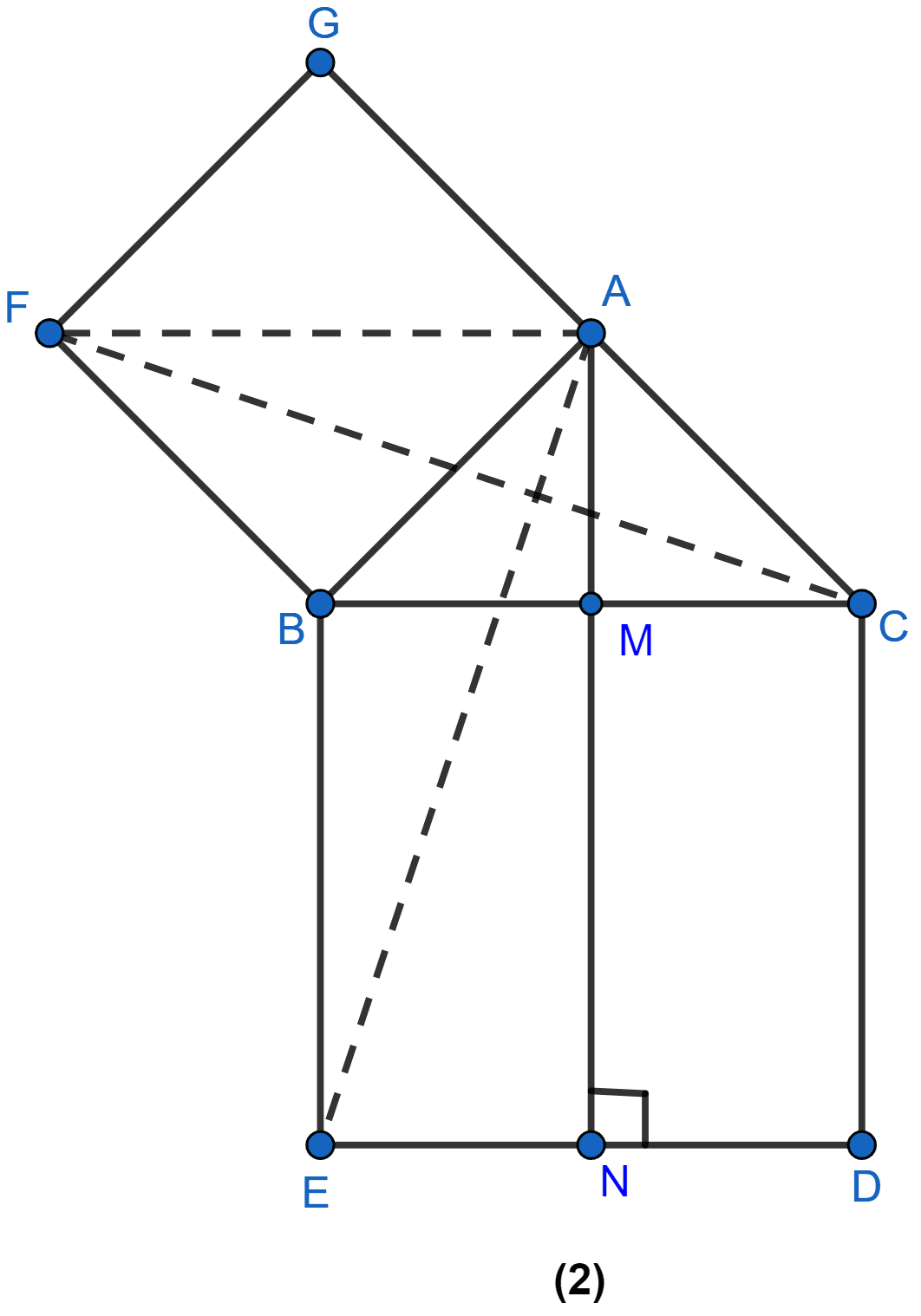
In figure (2) given below, ABC is a right-angled triangle at A. AGFB is a square on the side AB and BCDE is a square on the hypotenuse BC. If AN ⊥ ED, prove that
(i) ∆BCF ≅ ∆ABE.
(ii) area of square ABFG = area of rectangle BENM.
Related Questions
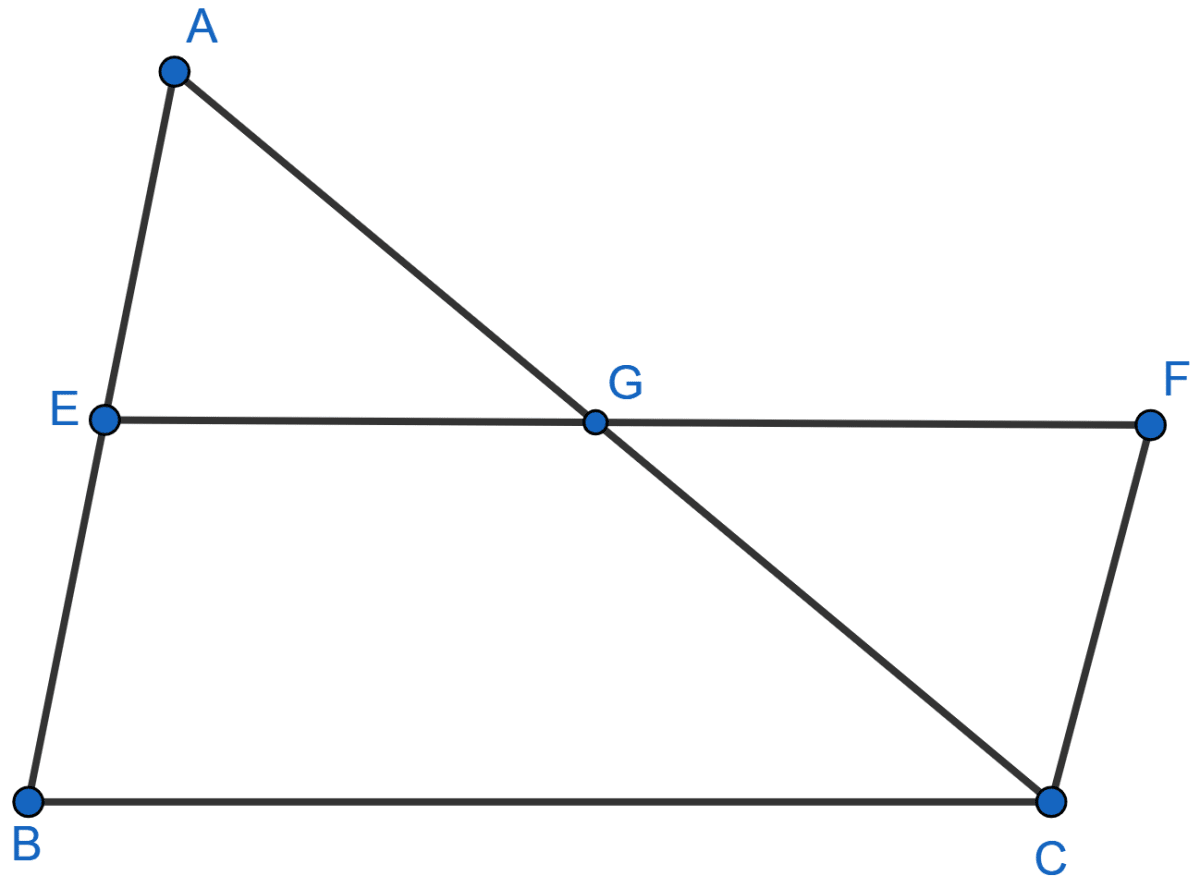
In the adjoining figure, E is the midpoint of the side AB of a triangle ABC and EBCF is a parallelogram. If the area of ∆ ABC is 25 sq. units, find the area of || gm EBCF.
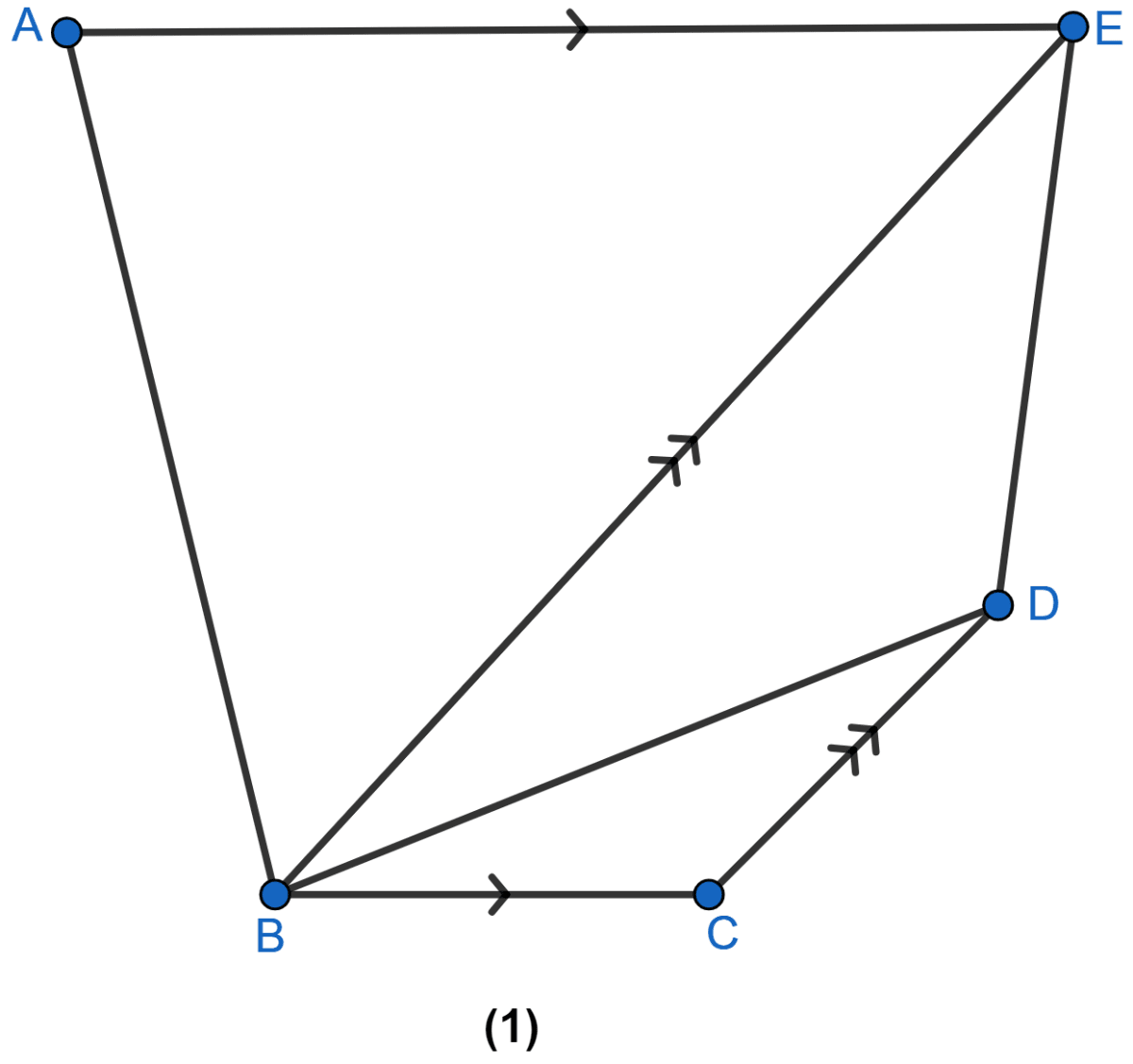
In the figure (1) given below, BC || AE and CD || BE. Prove that
area of ∆ABC= area of ∆EBD.
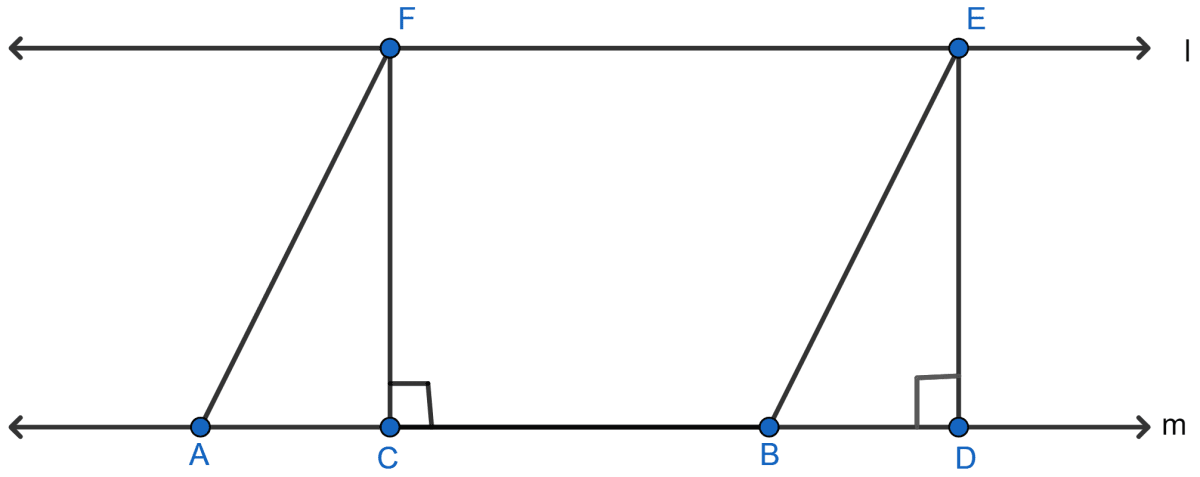
In the adjoining figure, if l || m, AF || BE, FC ⊥ m and ED ⊥ m, then the correct statement is
area of || ABEF = area of rect. CDEF
area of || ABEF = area of quad. CBEF
area of || ABEF = 2 area of △ACF
area of || ABEF = 2 area of △EBD
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is
1 : 2
1 : 1
2 : 1
3 : 1