Mathematics
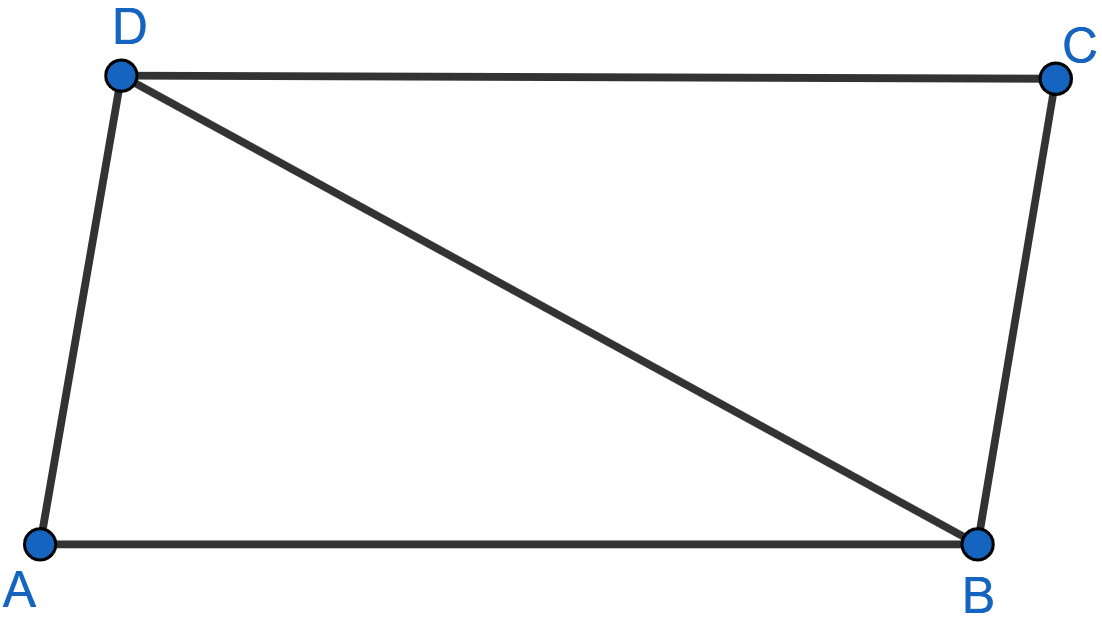
In the adjoining figure, AB = DC and AB || DC. Prove that AD = BC.
Triangles
159 Likes
Answer
In △ABD and △CDB,
AD = BC (Given)
∠ABD = ∠CDB (Alternate angles are equal)
BD = BD (Common sides)
∴ △ABD ≅ △CDB. (By SAS axiom)
We know that corresponding sides of congruent triangles are equal.
∴ AD = BC.
Hence, proved that AD = BC.
Answered By
85 Likes
Related Questions
In the adjoining figure, AD = BC and BD = AC. Prove that:
∠ADB = ∠BCA and ∠DAB = ∠CBA.

In the adjoining figure, ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that
(i) △ABD ≅ △BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
In the adjoining figure AC = AE, AB = AD and ∠BAD = ∠CAE. Show that BC = DE.

In the adjoining figure, AB = AC and D is the midpoint of BC. Use SSS rule of congruency to show that
(i) △ABD ≅ △ACD
(ii) AD is bisector of ∠A
(iii) AD is perpendicular to BC.
