Mathematics
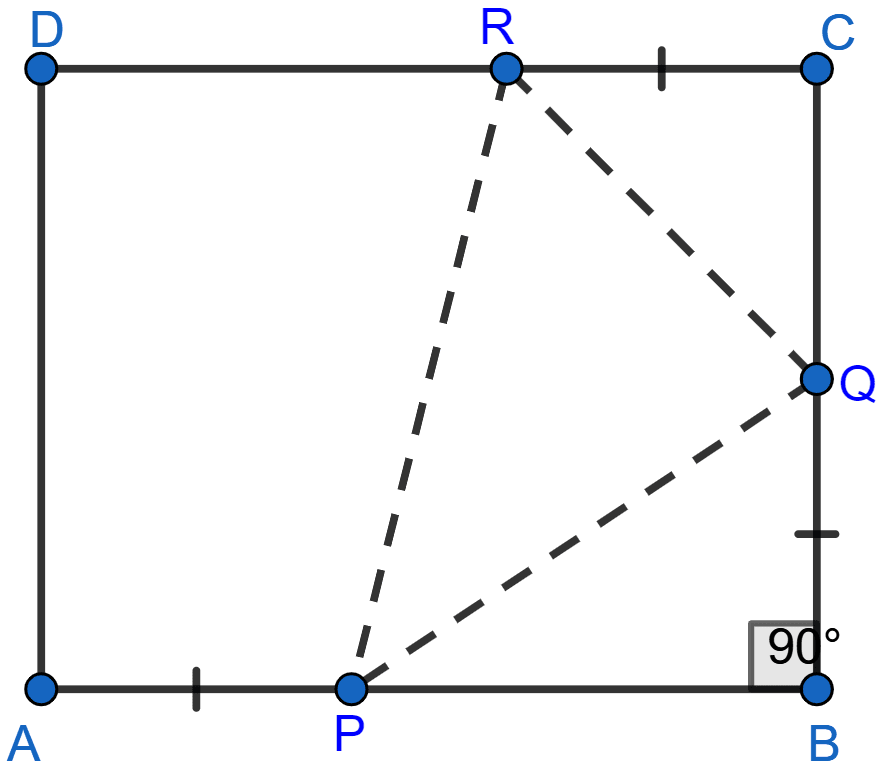
In the adjoining figure, ABCD is a square. P, Q and R are points on the sides AB, BC and CD respectively such that AP = BQ = CR and ∠PQR = 90°. Prove that
(a) △PBQ ≅ △QCR
(b) PQ = QR
(c) ∠PRQ = 45°
Triangles
49 Likes
Answer
(a) Given, ABCD is a square.
∴ AB = BC.
Given, AP = BQ.
∴ AB - AP = BC - BQ …….(i)
In △PBQ and △QCR,
BQ = CR (Given)
From (i) we get,
PB = QC
∠PBQ = ∠QCR (Both are equal to 90°, as each angle in square = 90°.)
Hence, proved △PBQ ≅ △QCR by SAS axiom.
(b) We know that corresponding parts of congruent triangles are equal.
∴ PQ = QR.
Hence, proved that PQ = QR.
(c) Considering △PQR.
We know PQ = QR and ∠Q = 90°.
Hence, △PQR is an isosceles triangle with ∠P = ∠R = x.
Sum of angles of triangle = 180°.
⇒ ∠P + ∠Q + ∠R = 180°
⇒ x + 90° + x = 180°
⇒ 2x = 90°
⇒ x = 45°.
Hence, proved that ∠PRQ = 45°.
Answered By
26 Likes
Related Questions
Assertion (A): Δ ABC ≅ Δ PQR
If 2AB = 3BC = 4CA = 12 cm, then the sum of perimeter of both triangle is 26 cm.
Reason (R): If two triangles are congruent to each other, then their corresponding sides are equal in length.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
In triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF. Will the two triangles be congruent? Give reasons for your answer.
In the adjoining figure, OA ⊥ OD, OC ⊥ OB, OD = OA and OB = OC. Prove that AB = CD.

In the adjoining figure, PQ || BA and RS || CA. If BP = RC, prove that:
(i) △BSR ≅ △PQC
(ii) BS = PQ
(iii) RS = CQ.
