Mathematics
In the adjoining figure, ABCD is a trapezium in which AB || DC. If 2AB = 3DC, find the ratio of the areas of △AOB and △COD.

Similarity
20 Likes
Answer
Given, 2AB = 3DC
.
Considering △AOB and △COD,
∠AOB = ∠COD (Vertically opposite angles are equal)
∠OAB = ∠OCD (Alternate angles are equal)
Hence by AA axiom △AOB ~ △COD.
We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, the ratio of area of △AOB : area of △COD is 9 : 4.
Answered By
11 Likes
Related Questions
In the adjoining figure, D is a point on BC such that ∠ABD = ∠CAD. If AB = 5 cm, AC = 3 cm and AD = 4 cm, find
(i) BC
(ii) DC
(iii) area of △ACD : area of △BCA

In the adjoining figure, the diagonals of a parallelogram intersect at O. OE is drawn parallel to CB to meet AB at E, find area of △AOE : area of ||gm ABCD.
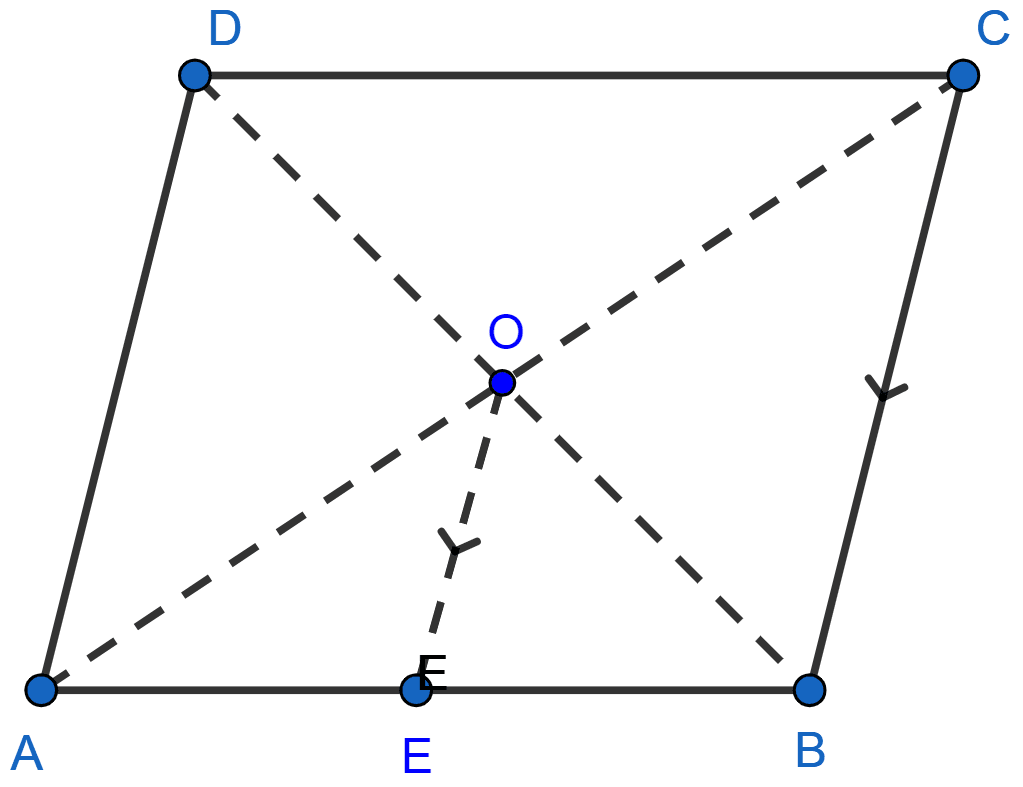
In the adjoining figure, ABCD is a parallelogram. E is mid-point of BC. DE meets the diagonal AC at O and meet AB (produced) at F. Prove that
(i) DO : OE = 2 : 1
(ii) area of △OEC : area of △OAD = 1 : 4
In the given diagram ∆ADB and ∆ACB are two right angled triangles with ∠ADB = ∠BCA = 90°. If AB = 10 cm, AD = 6 cm, BC = 2.4 cm and DP = 4.5 cm

(a) Prove that ∆APD ∼ ∆BPC.
(b) Find the length of BD and PB
(c) Hence, find the length of PA
(d) Find area ∆APD : area ∆BPC