Mathematics
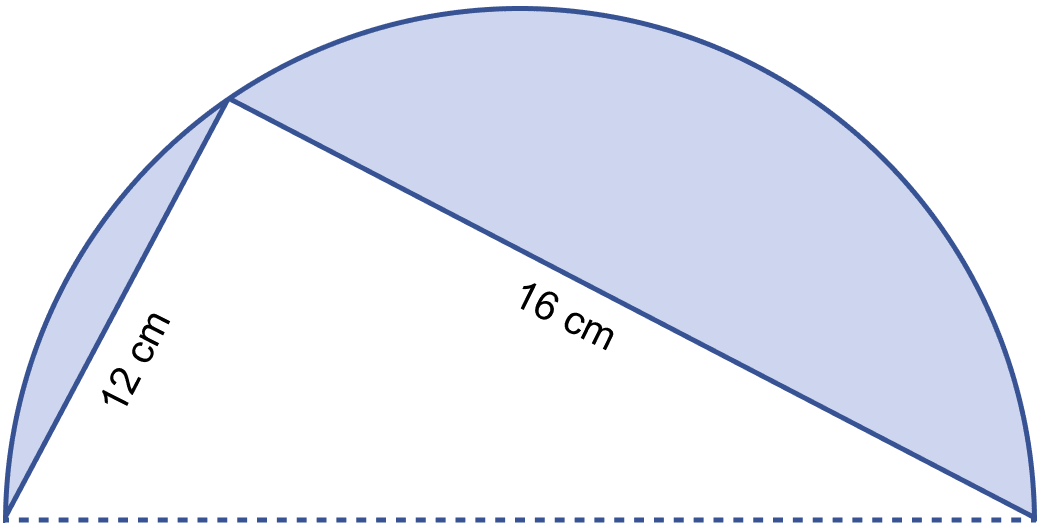
In the adjoining figure, O is the center of a circular arc and AOB is a line segment. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
Mensuration
16 Likes
Answer
Angle in semi-circle = 90°
∴ ∠ACB = 90°
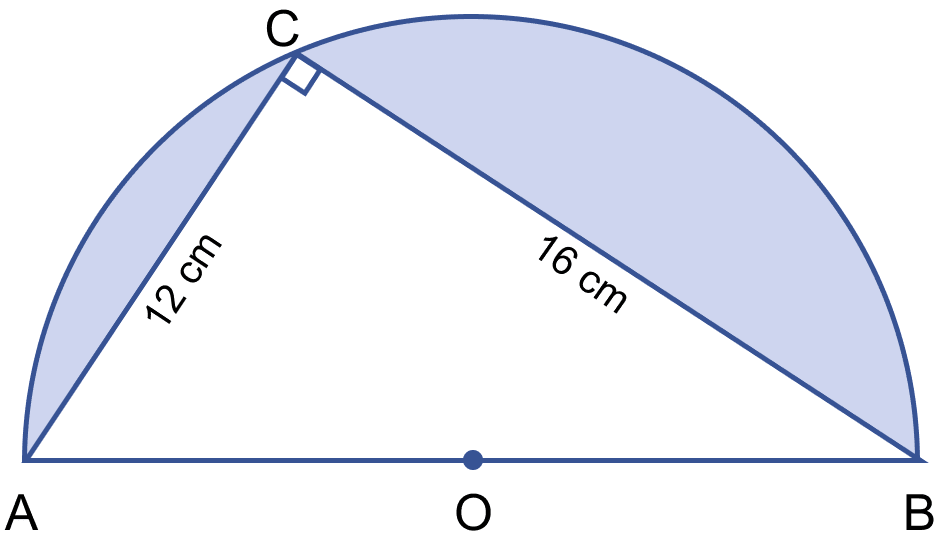
Using pythagoras theorem,
⇒ AB2 = AC2 + BC2
⇒ AB2 = 122 + 162
⇒ AB2 = 144 + 256
⇒ AB2 = 400
⇒ AB = = 20 cm.
AB is the diameter of circle,
∴ Radius = = = 10 cm.
Area of shaded region = Area of semi-circle - Area of triangle
Perimeter of shaded region = Circumference of semi-circle + AC + CB
= πr + 12 + 16
= 3.142 × 10 + 28
= 31.42 + 28
= 59.42 cm.
Hence, perimeter of shaded region = 59.42 cm and area of semi-circle = 61.1 cm2.
Answered By
9 Likes
Related Questions
A road 3.5 m wide surrounds a circular park whose circumference is 88 m. Find the cost of paving the road at the rate of ₹60 per square metre.
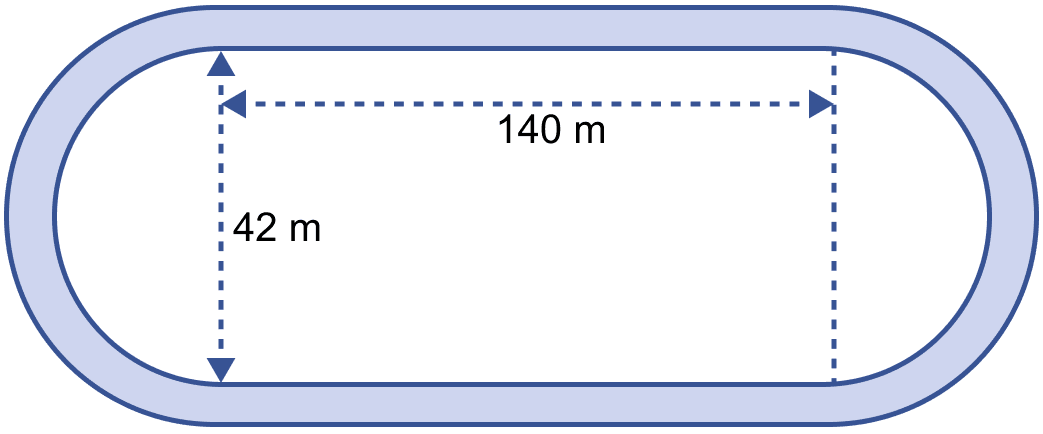
The adjoining sketch shows a running track 3.5 m wide all around which consists of two straight paths and two semicircular rings. Find the area of the track.
In the figure (i) given below, the radius is 3.5 cm. Find the perimeter of the quarter of the circle.

In the figure (ii) given below, there are five squares each of side 2 cm.
(i) Find the radius of the circle.
(ii) Find the area of the shaded region. (Take π = 3.14).
