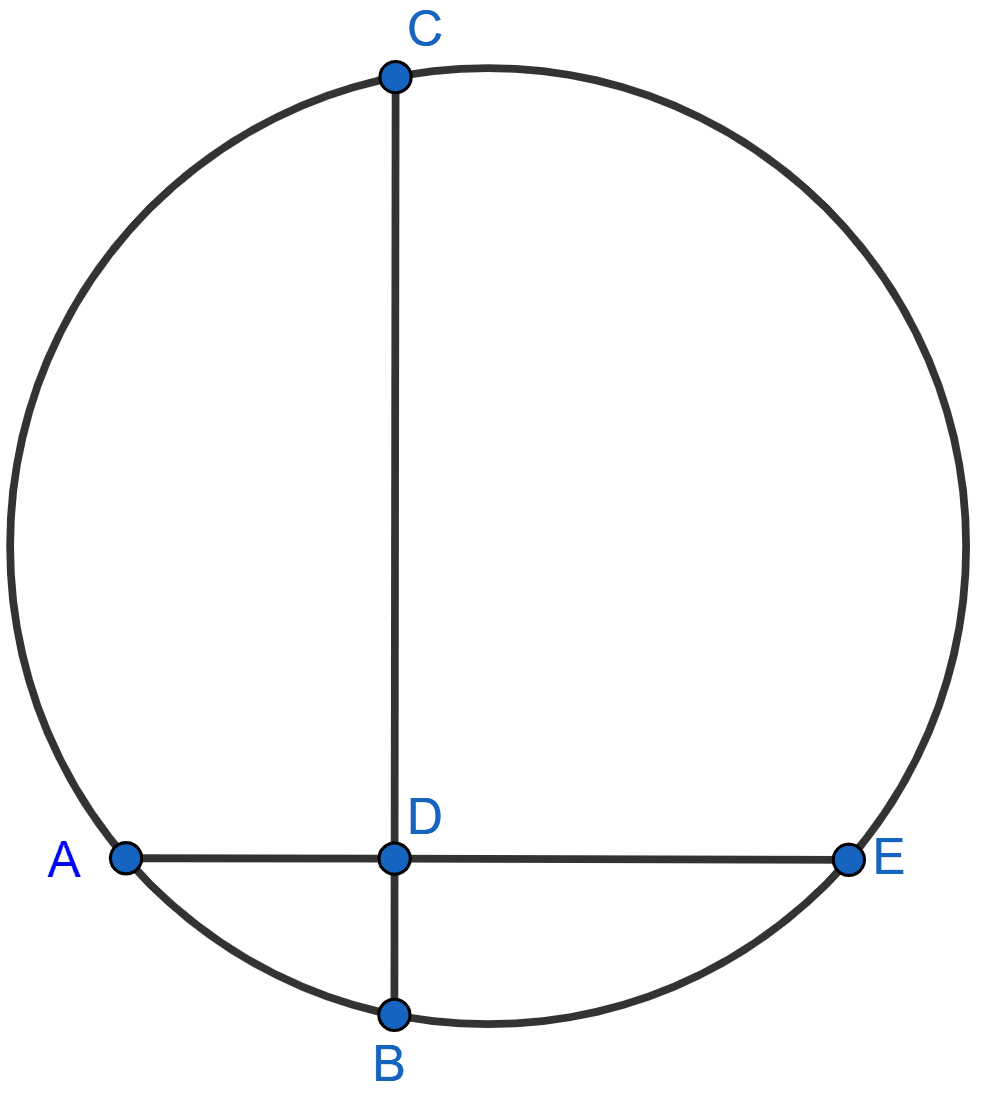
In the figure, chords AE and BC intersect each other at point D.

(i) If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE.

(ii) If AD = BD, show that : AE = BC.

(i) Join AB.

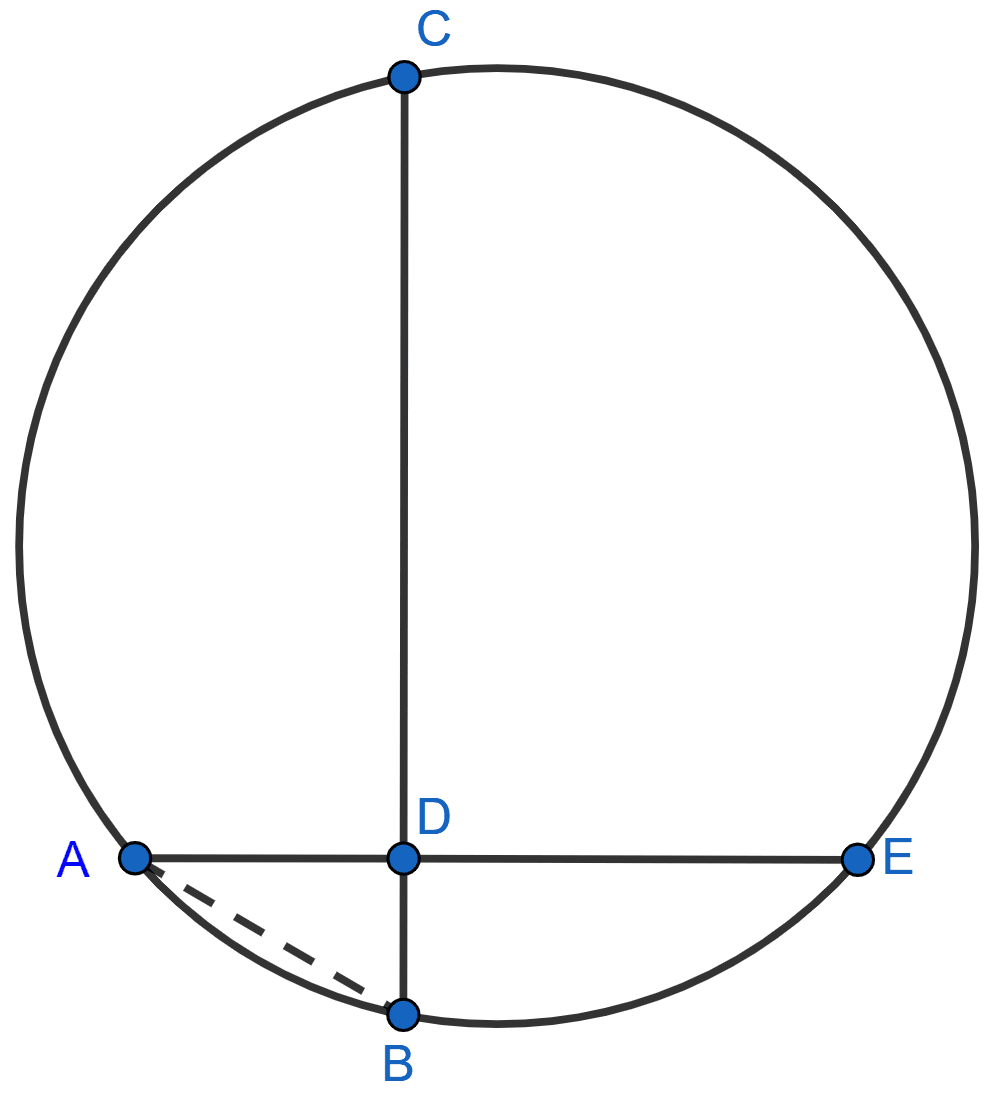
∠ADB = ∠CDE = 90° [Vertically opposite angles are equal.]

In right angle triangle ADB,

⇒ AB² = AD² + BD²

⇒ 5² = AD² + 4²

⇒ 25 = AD² + 16

⇒ AD² = 25 - 16

⇒ AD² = 9

⇒ AD = $\sqrt{9}$

⇒ AD = 3 cm.

We know that,

If two chords of a circle intersect internally or externally then the product of the lengths of their segment is equal.

From figure,

Chords AE and CB intersect internally at point D.

⇒ AD × DE = CD × BD

⇒ 3 × DE = 4 × 9

⇒ DE = $\dfrac{36}{3}$

⇒ DE = 12 cm.

Hence, DE = 12 cm.

(ii) Given,

AD = BD ……..(1)

AD = BD = x (let)

We know that,

⇒ AD × DE = CD × BD

⇒ (x)DE = (x)CD

⇒ DE = CD ……….(2)

Adding (1) and (2), we get :

⇒ AD + DE = BD + CD

⇒ AE = BC.

Hence, proved that AE = BC.