Mathematics
In the figure (ii) given below, chords BA and DC of a circle meet at P. Prove that
(i) ∠PAD = ∠PCB
(ii) PA × PB = PC × PD.

Circles
67 Likes
Answer
(i) From figure,
∠PAD + ∠DAB = ∠PCB + ∠BCD (∵ both are equal to 180°)….(i)
∠DAB = ∠BCD (∵ angles in same segment are equal.)
Putting this value of ∠DAB in (i) we get,
⇒ ∠PAD + ∠BCD = ∠PCB + ∠BCD
⇒ ∠PAD = ∠PCB + ∠BCD - ∠BCD
⇒ ∠PAD = ∠PCB
Hence, proved that ∠PAD = ∠PCB.
(ii) In △PBC and △PAD,
∠PAD = ∠PCB (Proved above.)
∠P = ∠P (Common angle.)
△PBC ~ △PAD. (By AA axiom)
Since triangles are similar hence, the ratio of corresponding sides are similar,
Hence proved that PA × PB = PC × PD.
Answered By
38 Likes
Related Questions
In adjoining figure, AB = 9 cm, PA = 7.5 cm and PC = 5 cm. Chords AD and BC intersect at P.
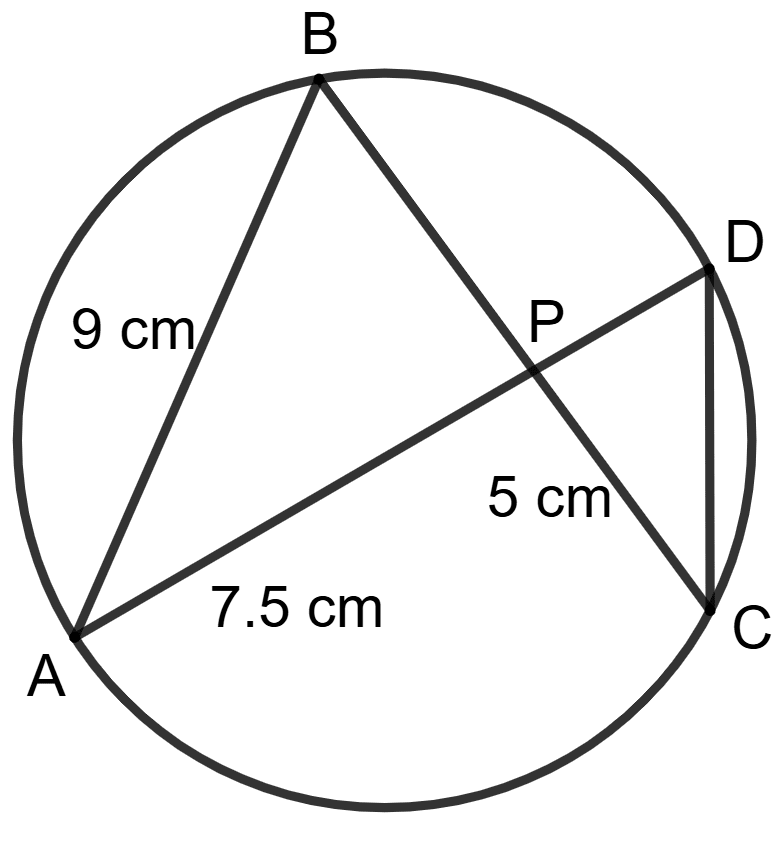
(i) Prove that Δ PAB ∼ Δ PCD.
(ii) Find the length of CD.
(iii) Find the area of Δ PAB : area of Δ PCD.
In the figure (i) given below, QPX is the bisector of ∠YXZ of the triangle XYZ. Prove that XY : XQ = XP : XZ.
If O is the center of the circle find the value of x in the following figure (using the given information) :

If O is the center of the circle find the value of x in the following figure (using the given information) :
