Mathematics
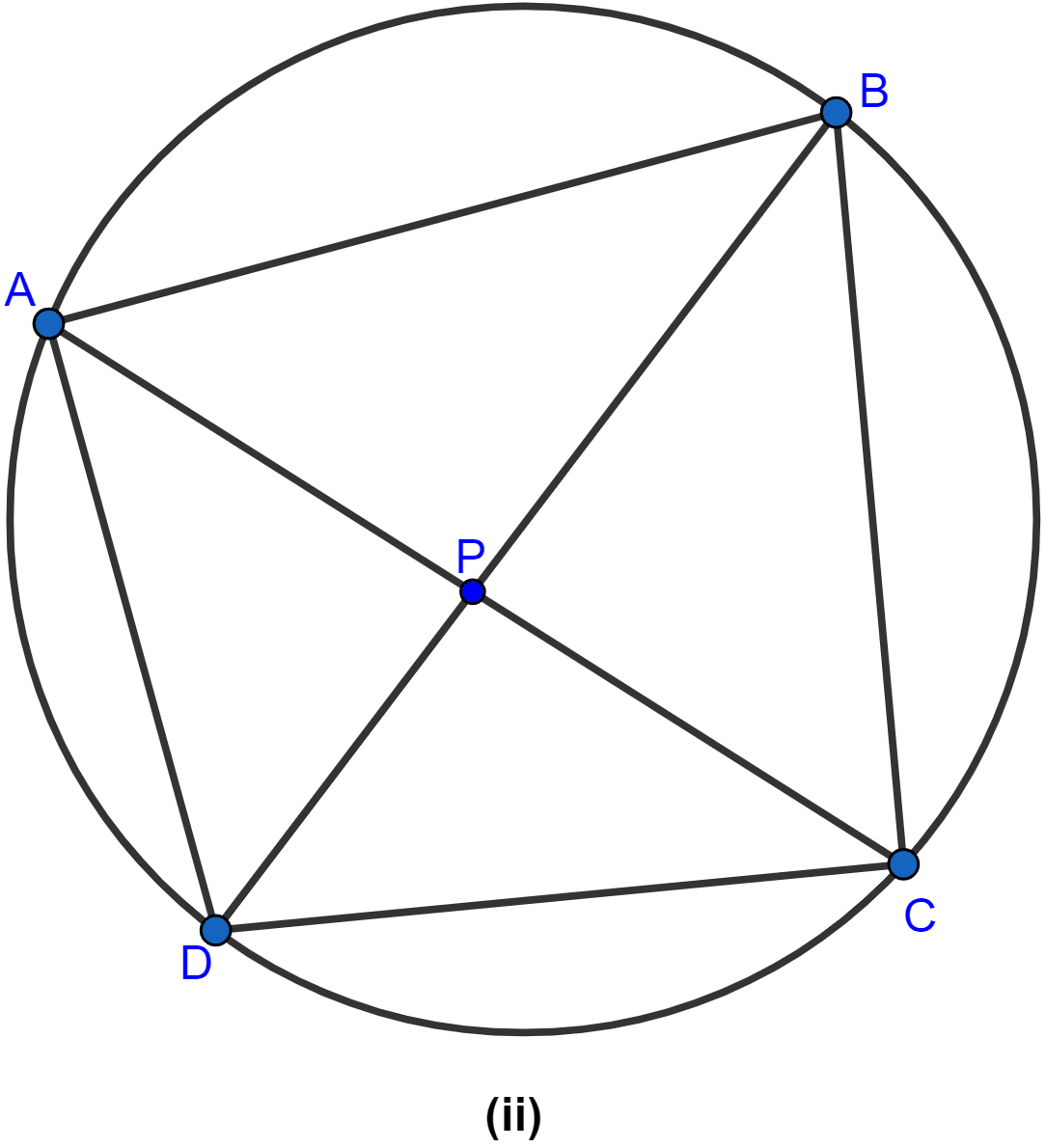
In the figure (ii) given below, the diagonals of a cyclic quadrilateral ABCD intersect in P and the area of the triangle APB is 24 cm2. If AB = 8 cm and CD = 5 cm, calculate the area of △DPC.
Circles
32 Likes
Answer
In △ABP and △DPC,
∠APB = ∠DPC (∵ vertically opposite angles are equal.)
∠ABP = ∠DCP (∵ angles in same segment are equal.)
△APB ~ △DPC. (By AA axiom)
We know that ratio of the area of similar triangles is the ratio of their corresponding sides.
Hence, the area of △DPC = cm2.
Answered By
17 Likes
Related Questions
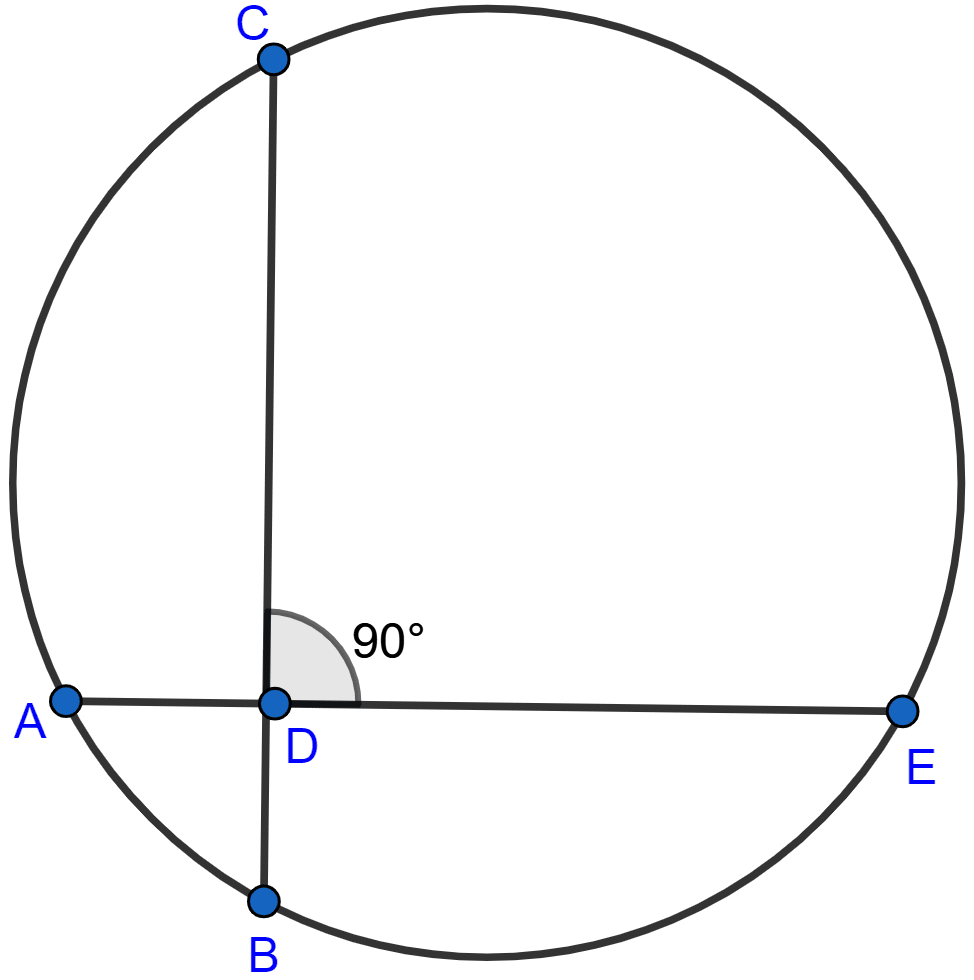
In the adjoining figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find DE.
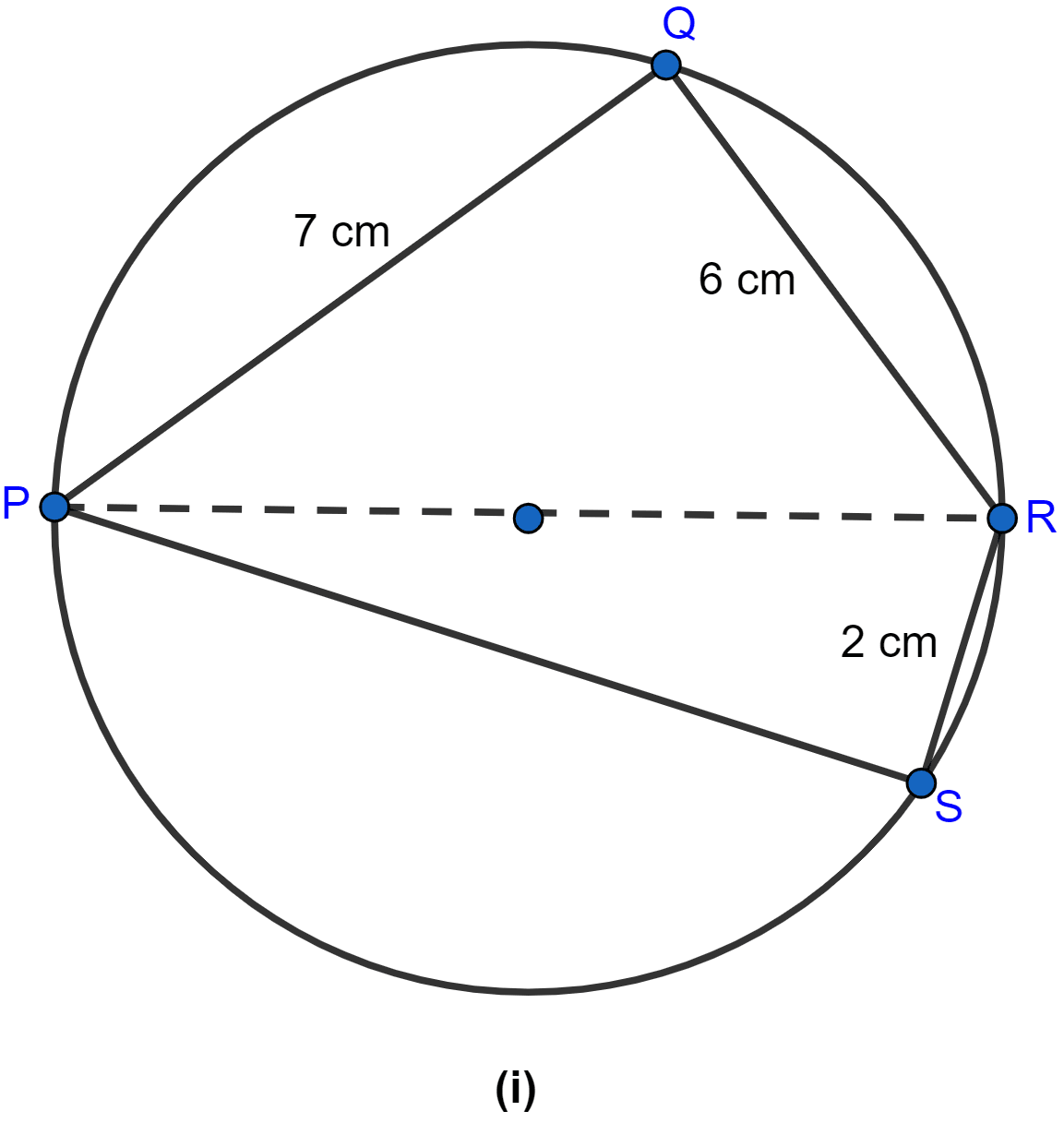
In the figure (i) given below, PR is a diameter of the circle, PQ = 7 cm, QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
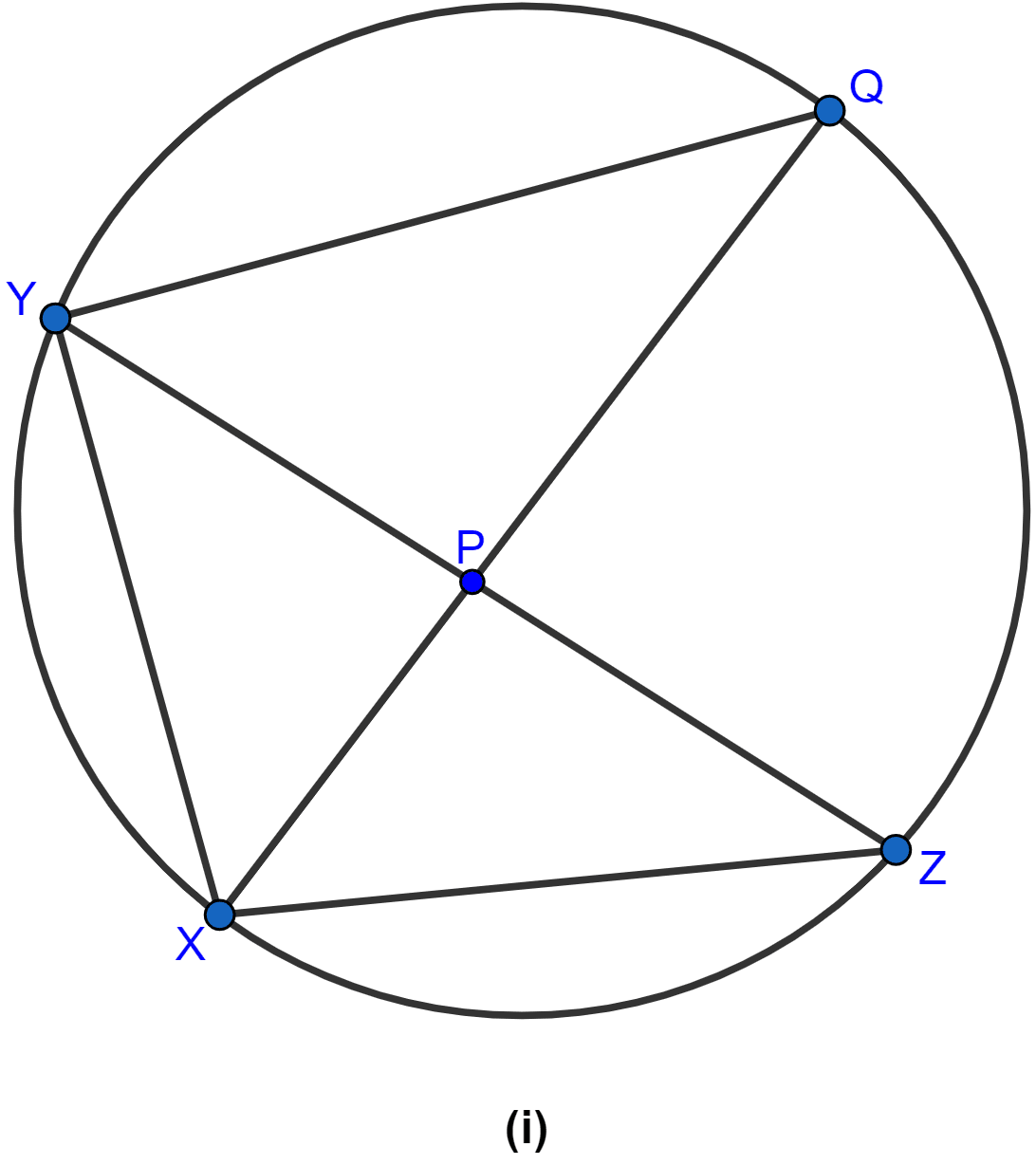
In adjoining figure, AB = 9 cm, PA = 7.5 cm and PC = 5 cm. Chords AD and BC intersect at P.
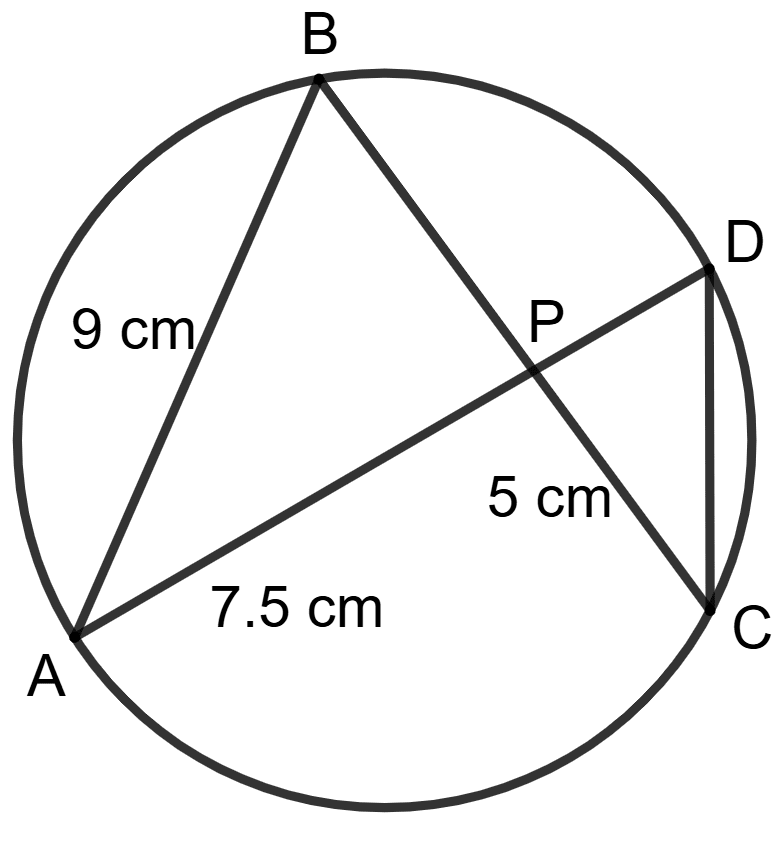
(i) Prove that Δ PAB ∼ Δ PCD.
(ii) Find the length of CD.
(iii) Find the area of Δ PAB : area of Δ PCD.
In the figure (i) given below, QPX is the bisector of ∠YXZ of the triangle XYZ. Prove that XY : XQ = XP : XZ.