Mathematics
In the figure of question 14, if E is the mid point of median AD, then prove that :
Area (△ ABE) = Area (△ ABC).
Theorems on Area
17 Likes
Answer
We know that,
Median of a triangle divides it into two triangles of equal area.
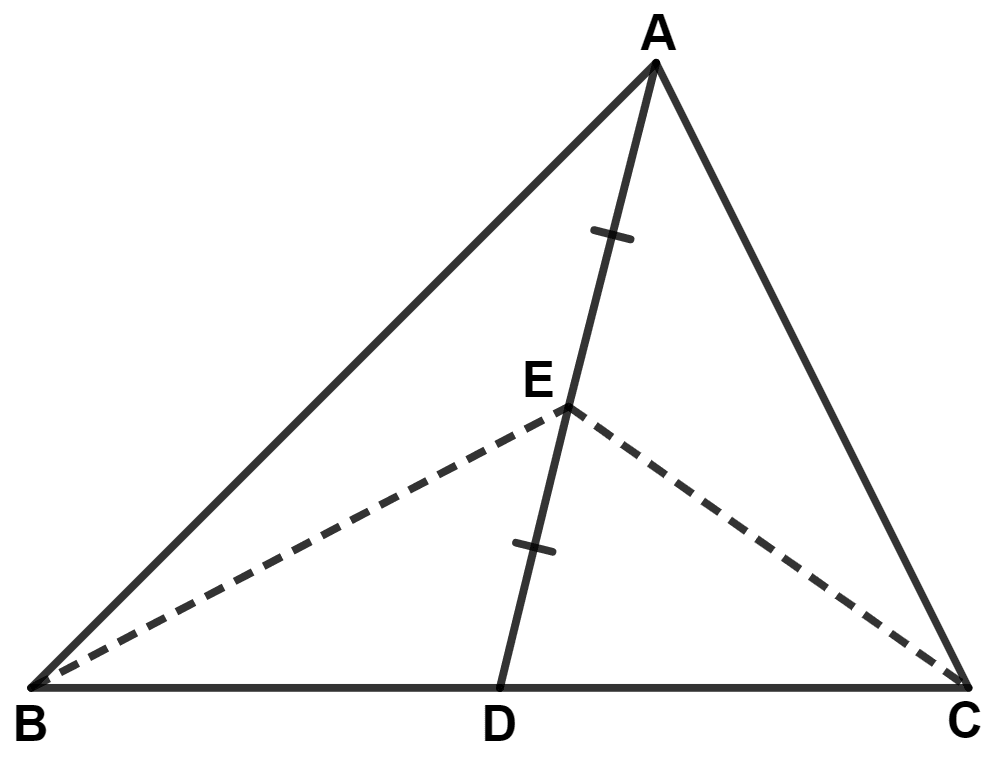
From figure,
AD is the median of Δ ABC, so it will divide Δ ABC into two equal triangles.
∴ Area of Δ ABD = Area of Δ ADC = Area of Δ ABC
⇒ Area of Δ ABD = Area of Δ ABC ………(1)
In Δ ABD,
Since, E is mid-point of AD,
∴ BE is the median.
∴ BE will divide Δ ABD into two equal triangles.
∴ Area of Δ ABE = Area of Δ BED = Area of Δ ABD
⇒ Area of Δ ABE = Area of Δ ABD ………(2)
Substituting value of Area of Δ ABD from equation (1) in (2), we get :
⇒ Area of Δ ABE = Area of Δ ABC
⇒ Area of Δ ABE = Area of Δ ABC.
Hence, proved that area of Δ ABE = area of Δ ABC.
Answered By
12 Likes
Related Questions
Show that :
(i) a diagonal divides a parallelogram into two triangles of equal area.
(ii) the ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
(iii) the ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
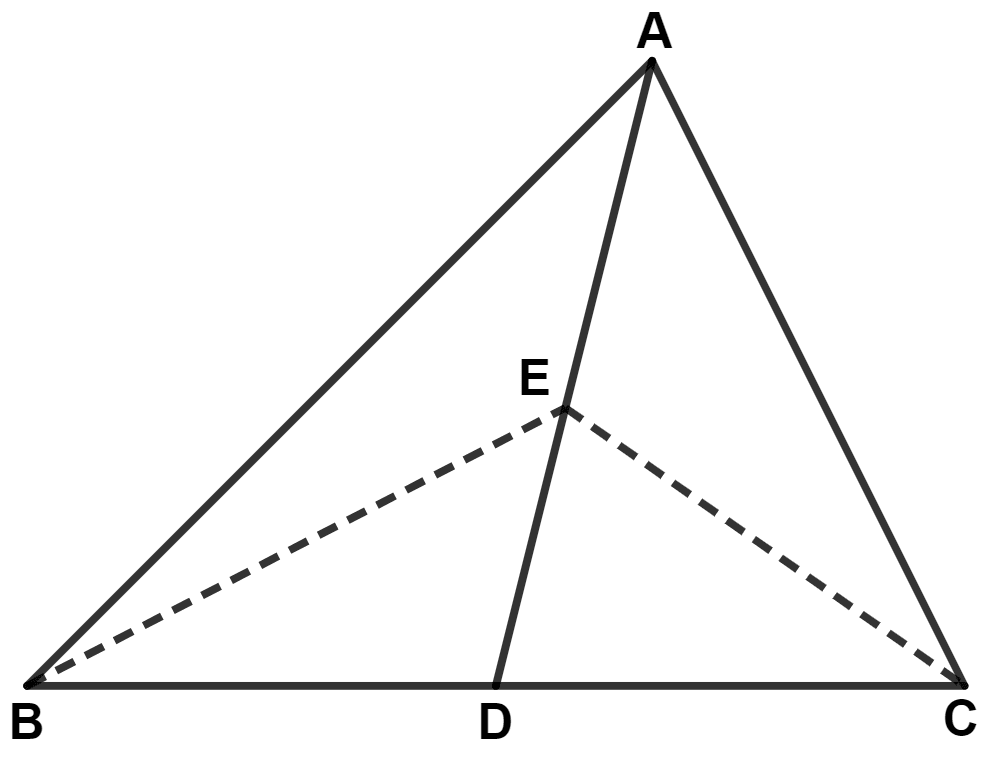
In the given figure; AD is median of △ ABC and E is any point on median AD. Prove that Area (△ ABE) = Area (△ ACE).
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively. Prove that area of triangle APQ = of the area of parallelogram ABCD.
The base BC of triangle ABC is divided at D so that BD = DC.
Prove that the area of Δ ABD = of the area of Δ ABC.