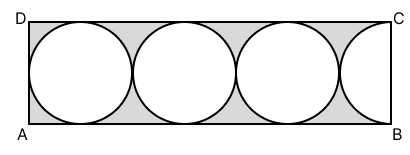
In the following figure, a rectangle ABCD encloses three circles. If BC = 14 cm, find the area of the shaded portion. $(\text{Take } \pi = 3\dfrac{1}{7})$

Given:

BC = 14 cm

AB = 14 + 14 + 14 + 7

= 49 cm

Area of shaded portion = Area of rectangle ABCD - (3 x Area of circle + Area of semicircle)

As we know, the area of rectangle = length x breadth

= 49 x 14 cm²

= 686 cm²

Diameter of the circle = 14 cm

Radius of the circle = $\dfrac{14}{2}$ cm = 7 cm

Area of the circle = πr²

$\text{Area of the circle} = \dfrac{22}{7} \times 7^2\\[1em] = \dfrac{22}{7} \times 49\\[1em] = \dfrac{1078}{7}\\[1em] = 154 \text{ cm}^2$

Area of 3 circles = 3 x 154 cm² = 462 cm²

Area of the semicircle = $\dfrac{1}{2}$πr²

$= \dfrac{1}{2} \times \dfrac{22}{7} \times 7^2\\[1em] = \dfrac{22}{14} \times 49\\[1em] = \dfrac{1078}{14}\\[1em] = 77 \text{ cm}^2$

⇒ Area of shaded portion = 686 - (462 + 77) cm²

= 686 - 539 cm²

= 147 cm²

Hence, the area of the shaded portion is 147 cm².