Mathematics
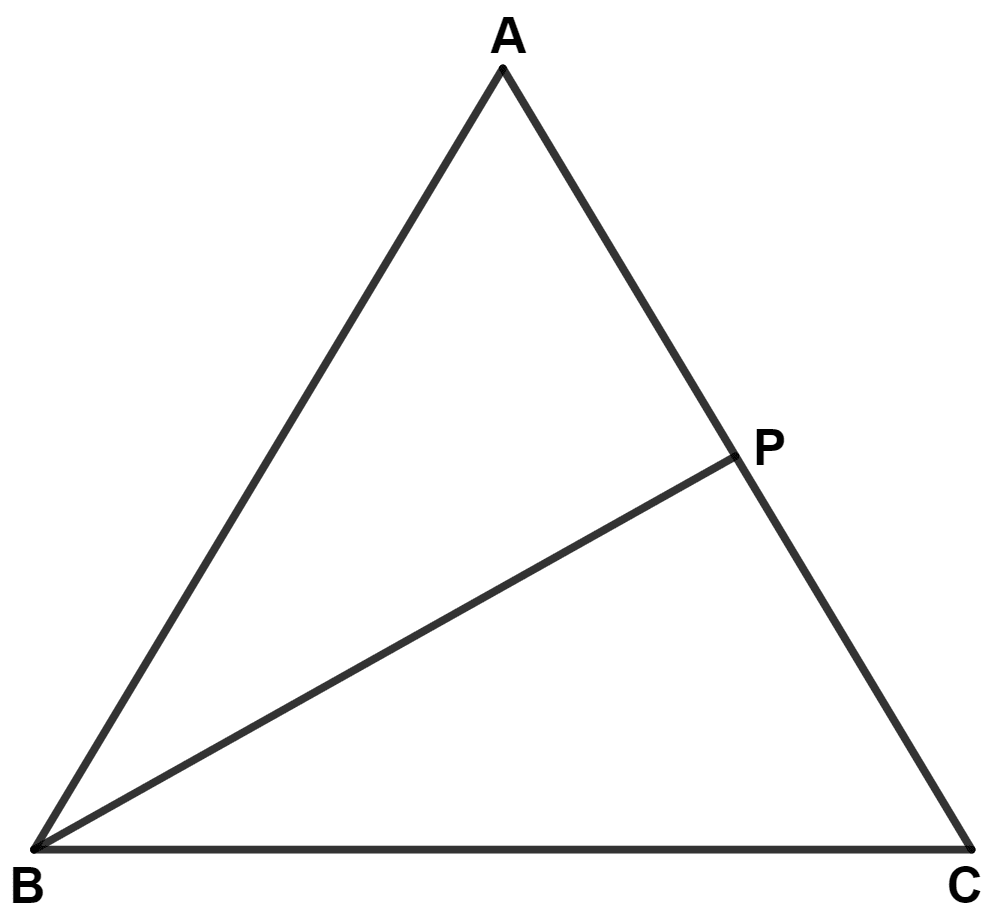
In the following figure, ABC is an equilateral triangle and P is any point in AC; prove that :
(i) BP > PA
(ii) BP > PC
Triangles
11 Likes
Answer
(i) Since, ABC is an equilateral triangle.
∴ ∠A = ∠B = ∠C = 60°.
In △ ABP,
∠ABP = ∠B - ∠PBC
∴ ∠ABP < ∠B
∴ ∠ABP < ∠A (Since, ∠B = ∠A)
∴ PA < BP or BP > PA [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.]
Hence, proved that BP > PA.
(ii) In △ BPC,
∠PBC = ∠B - ∠ABP
∴ ∠PBC < ∠B
∴ ∠PBC < ∠C (Since, ∠B = ∠C)
∴ PC < BP or BP > PC [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.]
Hence, proved that BP > PC.
Answered By
8 Likes
Related Questions
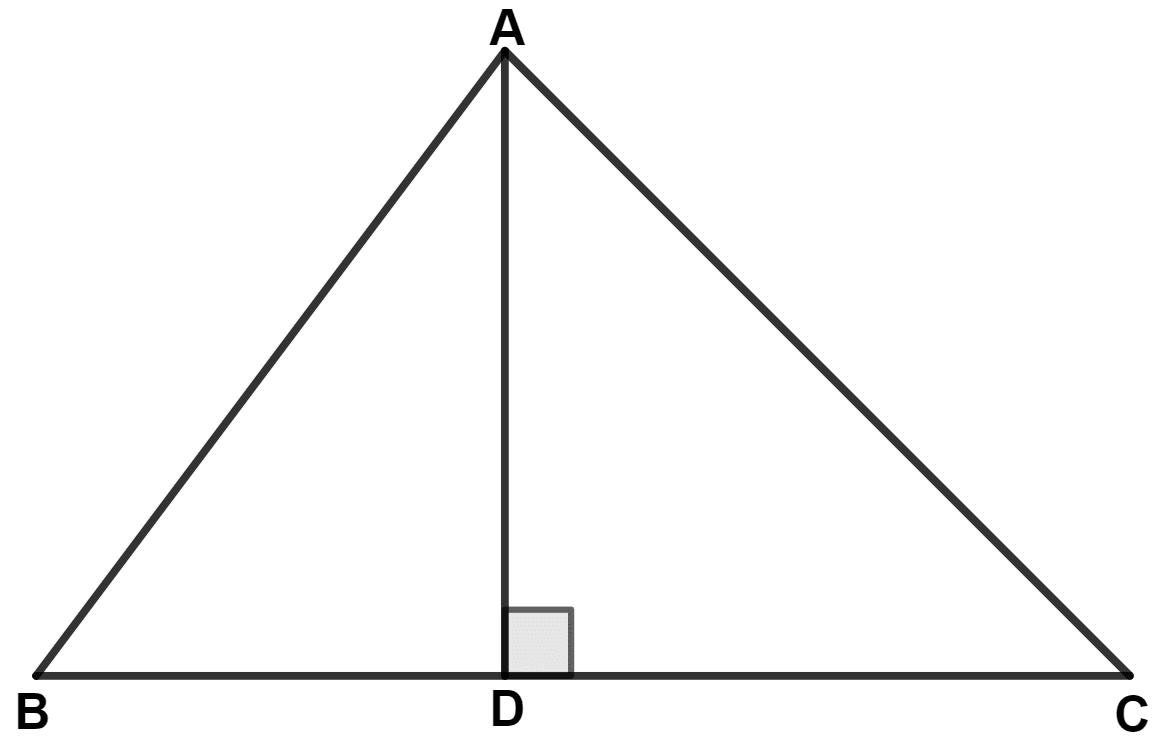
From the following figure; prove that :
(i) AB > BD
(ii) AC > CD
(iii) AB + AC > BC
In a quadrilateral ABCD; prove that :
(i) AB + BC + CD > DA
(ii) AB + BC + CD + DA > 2AC
(iii) AB + BC + CD + DA > 2BD
P is any point inside the triangle ABC. Prove that : ∠BPC > ∠BAC.
Prove that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.