Mathematics
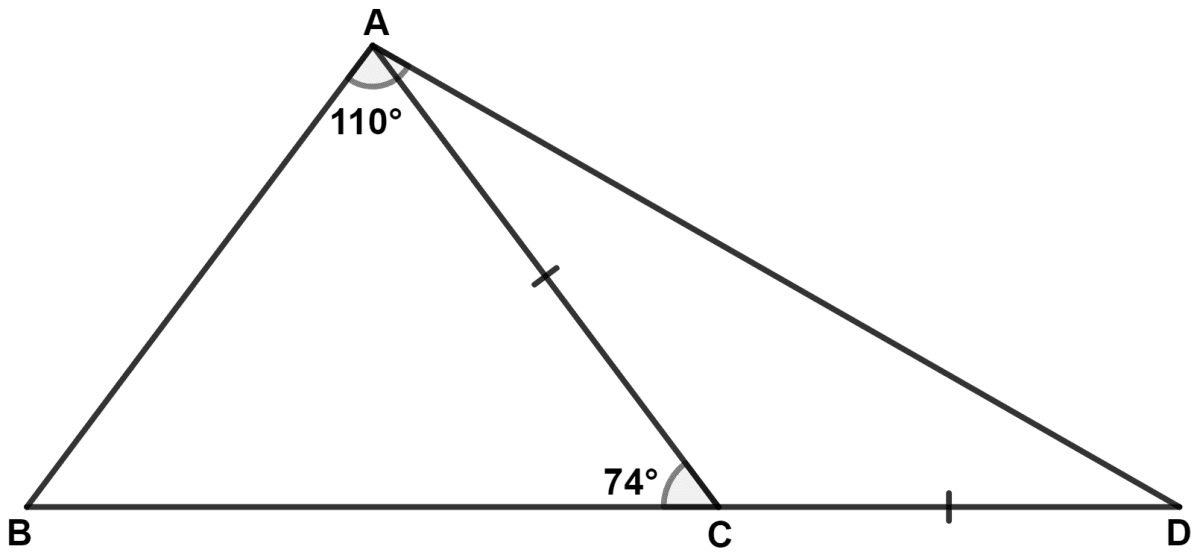
In the following figure;
AC = CD; ∠BAD = 110° and ∠ACB = 74°.
Prove that : BC > CD.
Triangles
15 Likes
Answer
Since, BCD is a straight line.
∴ ∠BCA + ∠ACD = 180°
⇒ 74° + ∠ACD = 180°
⇒ ∠ACD = 180° - 74° = 106°.
In △ ACD,
AC = CD (Given)
∴ ∠CAD = ∠CDA = x (let) [Angles opposite to equal sides are equal]
By angle sum property of triangle,
⇒ ∠ACD + ∠CAD + ∠CDA = 180°
⇒ 106° + x + x = 180°
⇒ 106° + 2x = 180°
⇒ 2x = 180° - 106°
⇒ 2x = 74°
⇒ x = = 37°.
From figure,
⇒ ∠BAC = ∠BAD - ∠CAD = 110° - 37° = 73°.
In △ ABC,
By angle sum property of triangle,
⇒ ∠BAC + ∠ABC + ∠ACB = 180°
⇒ 73° + ∠ABC + 74° = 180°
⇒ ∠ABC + 147° = 180°
⇒ ∠ABC = 180° - 147°
⇒ ∠ABC = 33°.
∴ ∠ACB > ∠BAC > ∠ABC
∴ AB > BC > AC [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.] …….(1)
Given,
AC = CD ……(2)
From equations (1) and (2), we get :
BC > CD.
Hence, proved that BC > CD.
Answered By
8 Likes
Related Questions
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
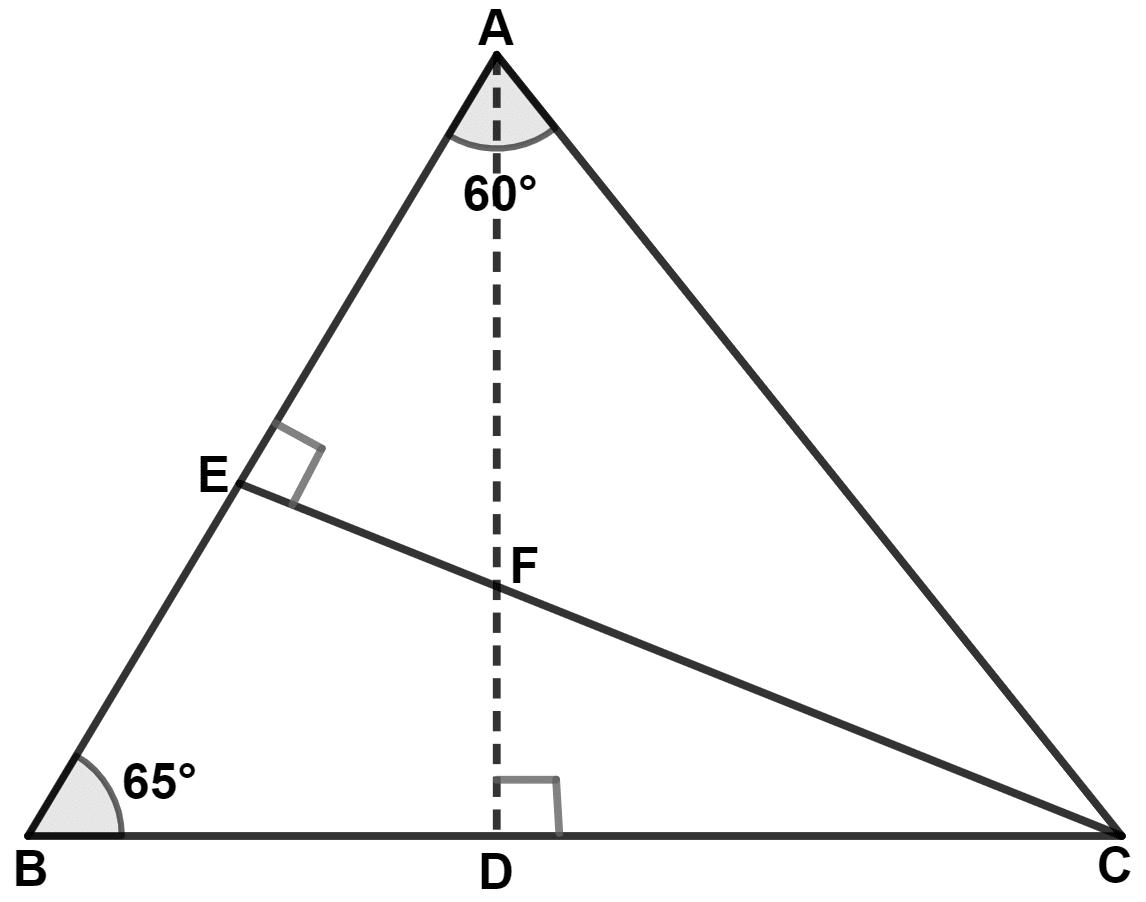
In the following figure, ∠BAC = 60° and ∠ABC = 65°. Prove that :
(i) CF > AF
(ii) DC > DF
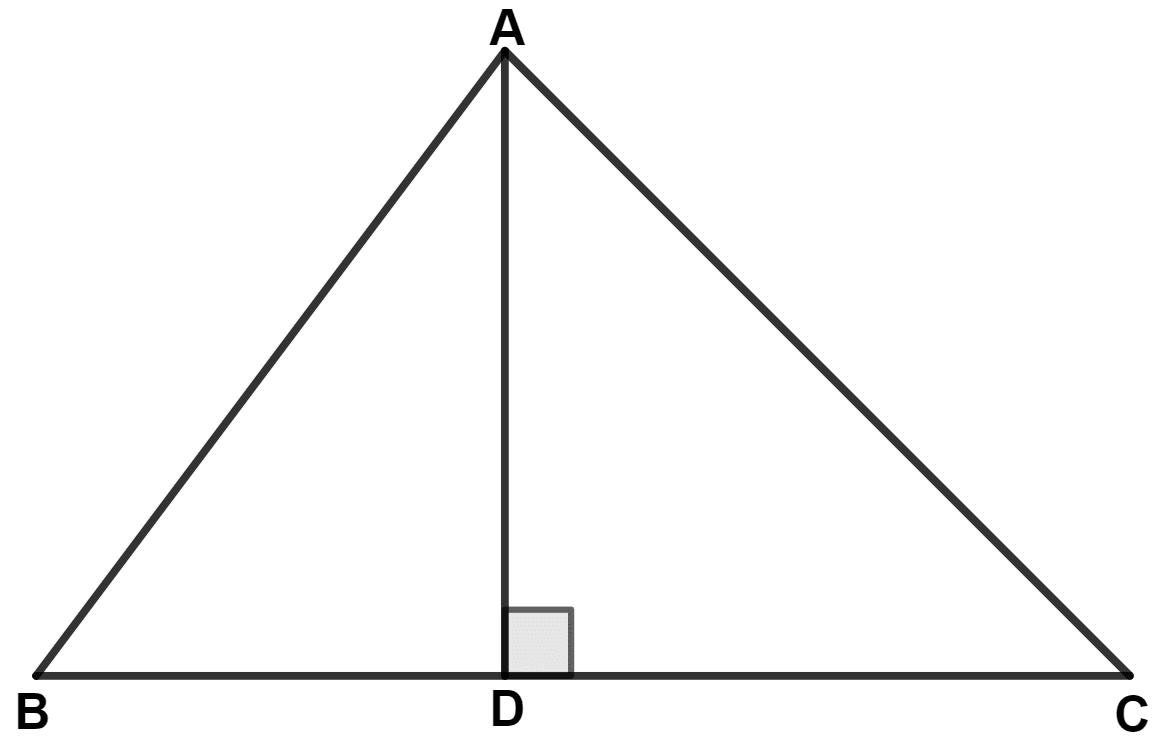
From the following figure; prove that :
(i) AB > BD
(ii) AC > CD
(iii) AB + AC > BC
In a quadrilateral ABCD; prove that :
(i) AB + BC + CD > DA
(ii) AB + BC + CD + DA > 2AC
(iii) AB + BC + CD + DA > 2BD