Mathematics
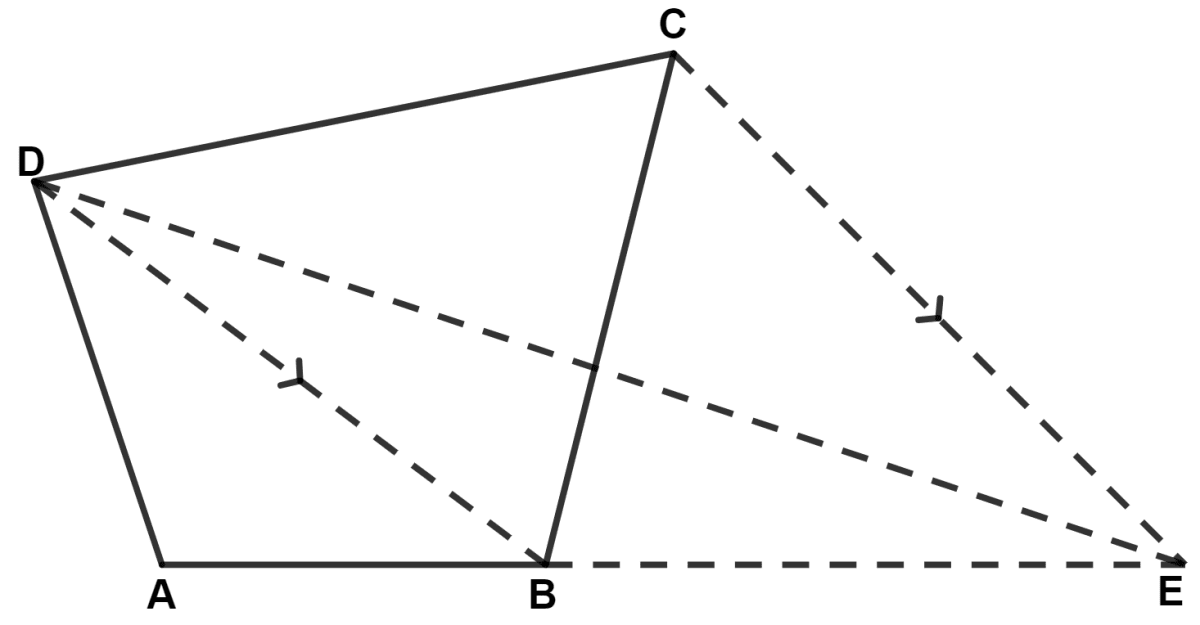
In the following figure, CE is drawn parallel to diagonal DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that △ ADE and quadrilateral ABCD are equal in area.
Theorems on Area
18 Likes
Answer
We know that,
Triangles on the same base and between the same parallel lines are equal in area.
△ BDE and △ BDC lie on the same base BD and along the same parallel lines DB and CE.
∴ Area of △ BDE = Area of △ BDC ……….(1)
From figure,
⇒ Area of △ ADE = Area of △ ADB + Area of △ BDE
⇒ Area of △ ADE = Area of △ ADB + Area of △ BDC [From equation (1)]
⇒ Area of △ ADE = Area of quadrilateral ABCD.
Hence, proved that △ ADE and quadrilateral ABCD are equal in area.
Answered By
10 Likes
Related Questions
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC. Prove that :
(i) △ CPD and △ AQD are equal in area.
(ii) Area (△ AQD) = Area (△ APD) + Area (△ CPB)
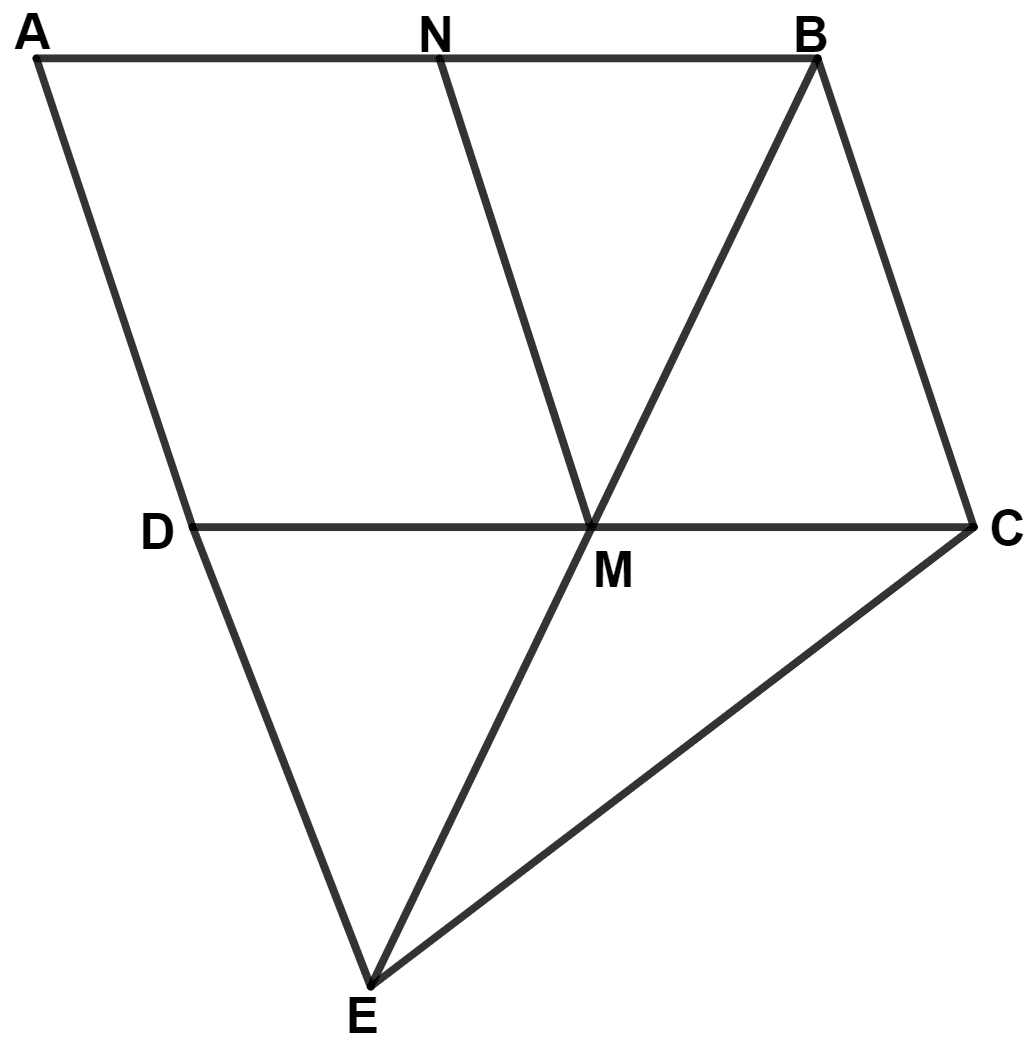
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is 48 cm2;
(i) state the area of the triangle BEC.
(ii) name the parallelogram which is equal in area to the triangle BEC.
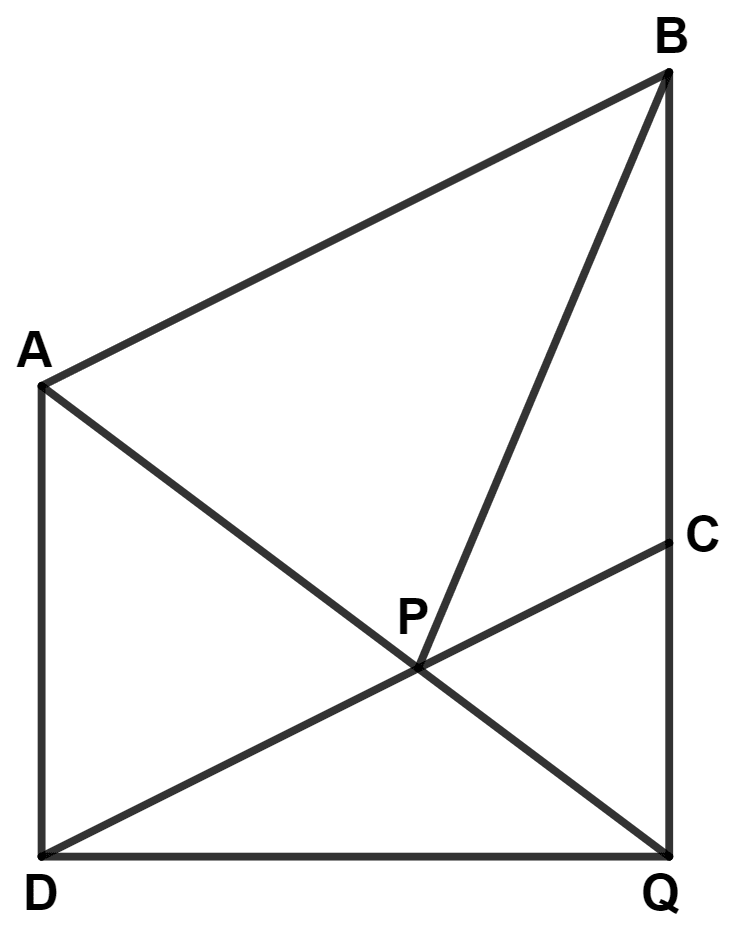
ABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
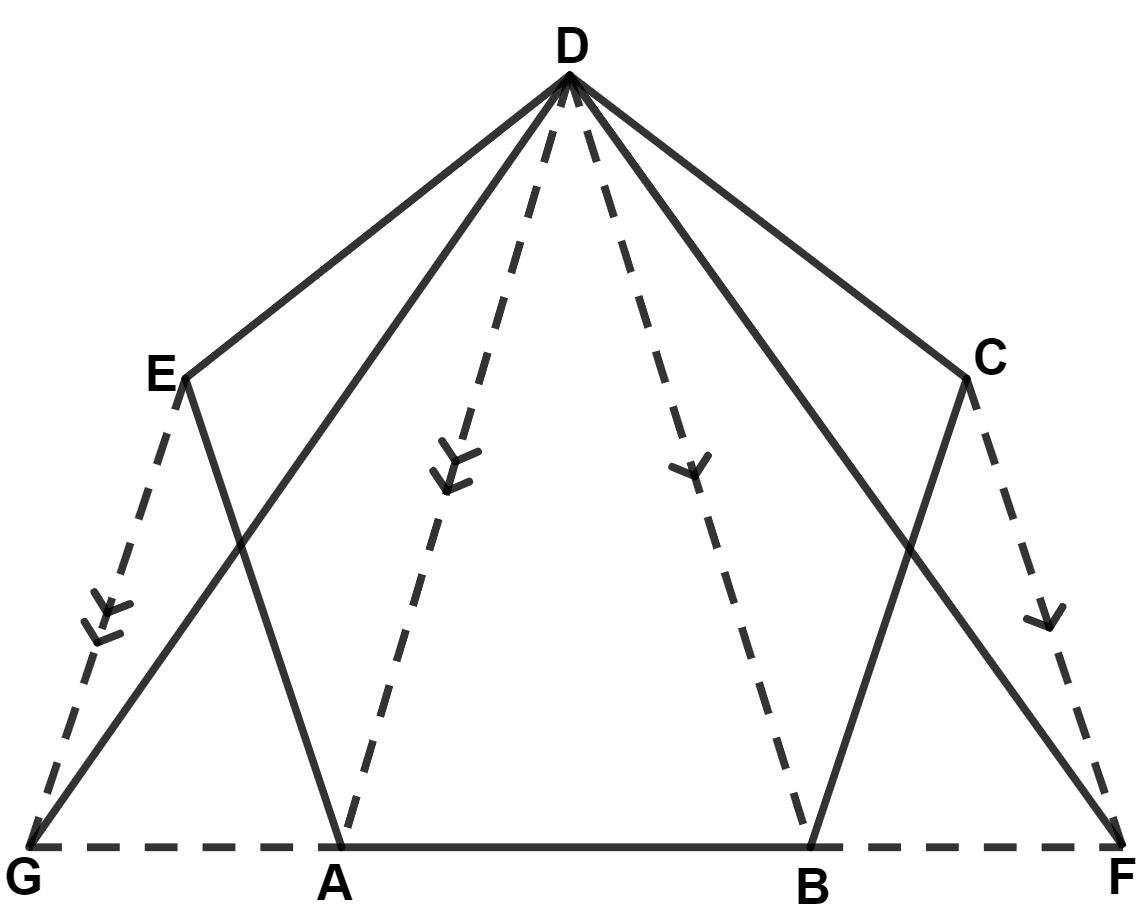
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.