Mathematics
In the following figure, OABC is a square. A circle is drawn with O as center which meets OC at P and OA at Q. Prove that :
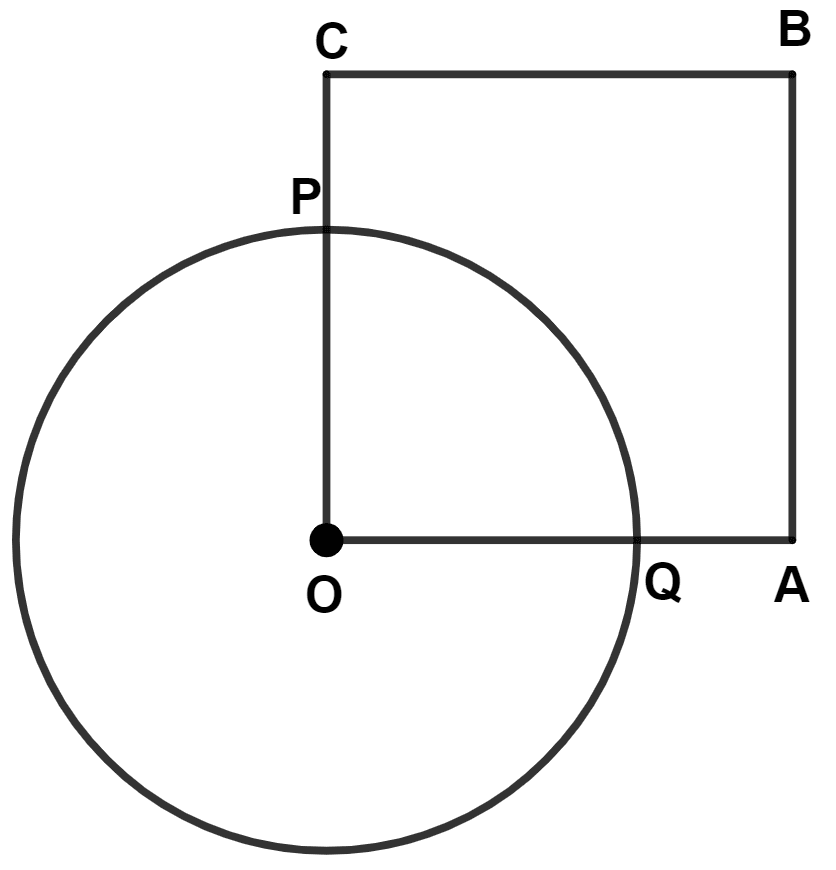
(i) △ OPA ≅ △ OQC
(ii) △ BPC ≅ △ BQA
Answer
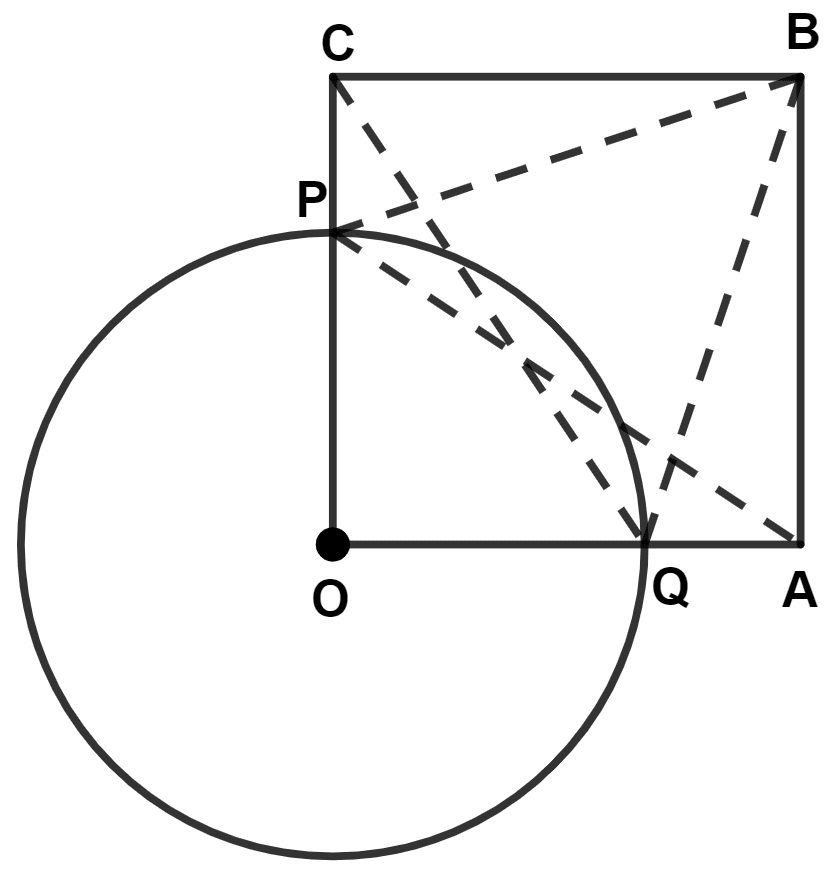
(i) In △ OPA and △ OQC,
⇒ OP = OQ (Radius of same circle)
⇒ ∠AOP = ∠COQ (Both equal to 90°)
⇒ OA = OC (Sides of square)
∴ △ OPA ≅ △ OQC (By S.A.S. axiom)
Hence, proved that △ OPA ≅ △ OQC.
(ii) Proved above,
⇒ OC = OA ………..(1)
⇒ OP = OQ ………..(2)
Subtracting equation (2) from (1),
⇒ OC - OP = OA - OQ
⇒ CP = QA
In △ BPC and △ BQA,
⇒ BC = BA (Sides of square)
⇒ ∠PCB = ∠QAB (Both equal to 90°)
⇒ CP = QA (Proved above)
∴ △ BPC ≅ △ BQA (By S.A.S. axiom)
Hence, proved that △ BPC ≅ △ BQA.
Related Questions
M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O. Prove that :
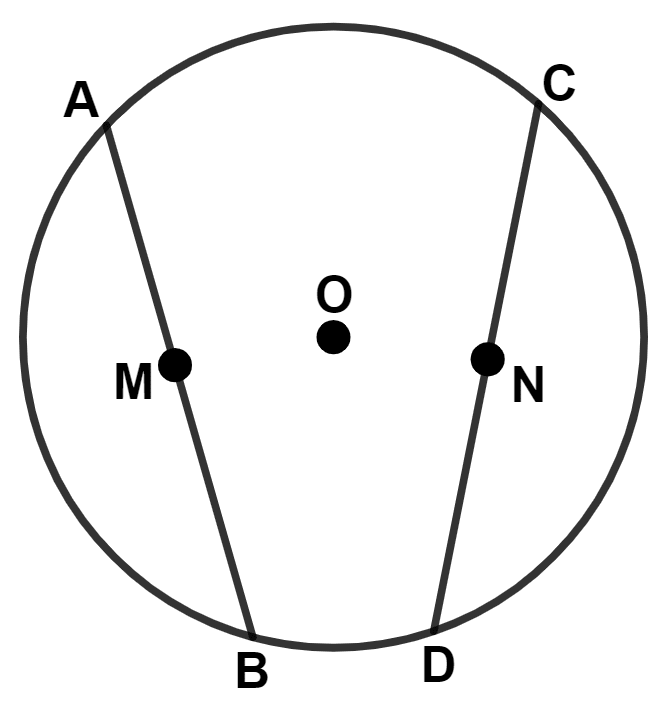
(i) ∠BMN = ∠DNM
(ii) ∠AMN = ∠CNM.
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle. Prove that :
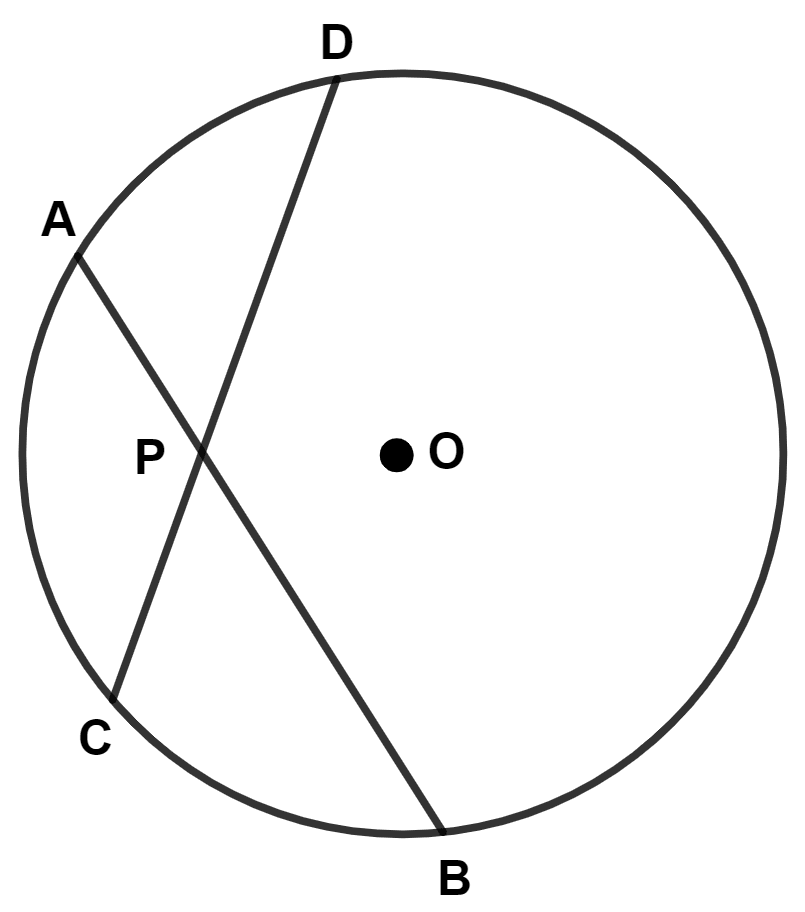
(i) AP = CP
(ii) BP = DP
The length of common chord of two intersecting circles is 30 cm. If the diameters of these two circles be 50 cm and 34 cm, calculate the distance between their centers.
The line joining the mid-points of two chords of a circle passes through its center. Prove that the chords are parallel.