Mathematics
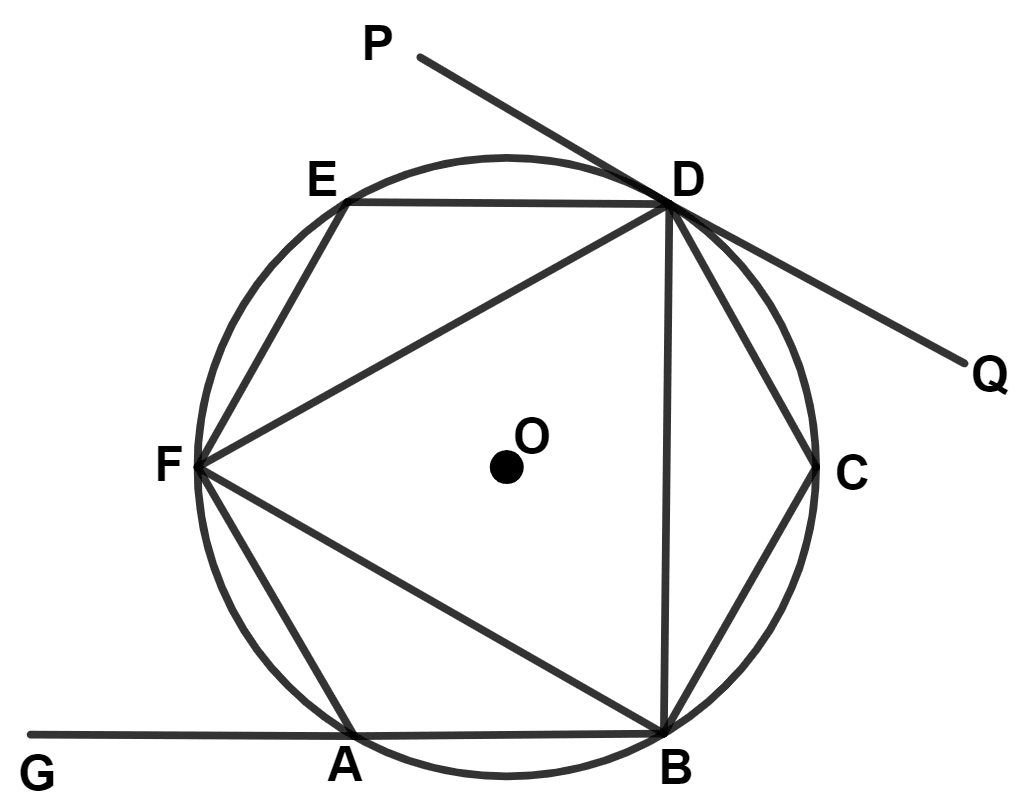
In the given diagram, ABCDEF is a regular hexagon inscribed in a circle with centre O. PQ is a tangent to the circle at D. Find the value of :
(a) ∠FAG
(b) ∠BCD
(c) ∠PDE
Circles
53 Likes
Answer
(a) By formula,
Each interior angle of a n sided polygon =
∴ ∠FAB = 120°
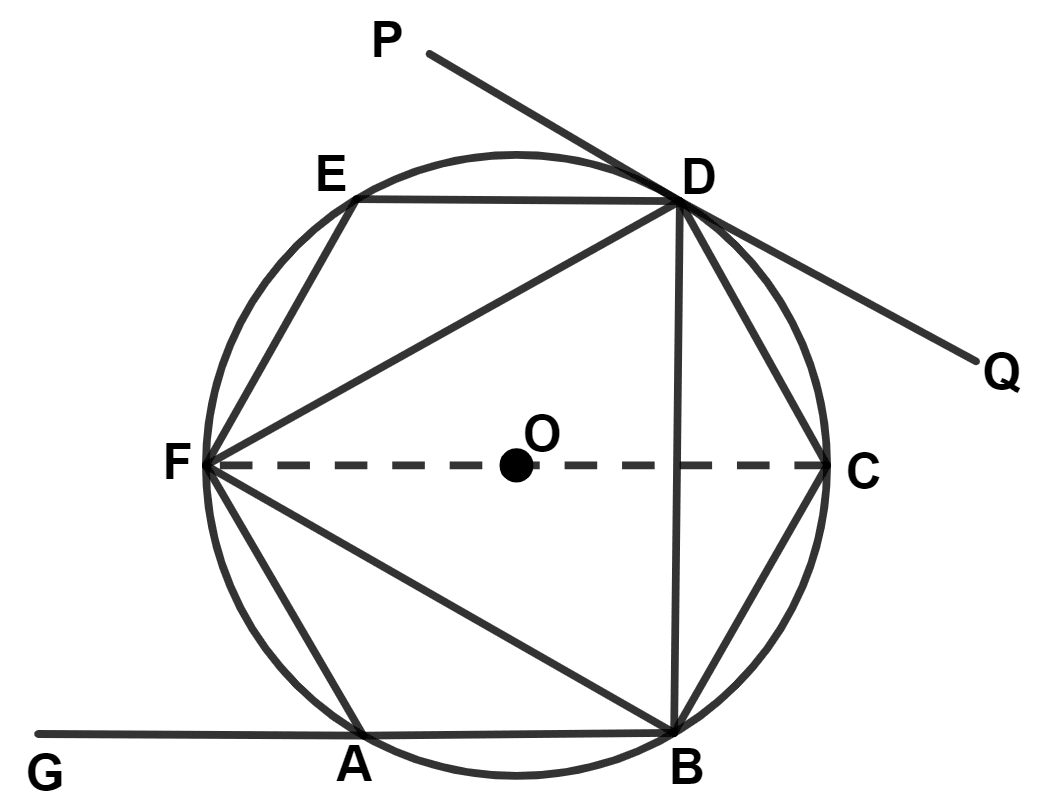
From figure,
∠FAG and ∠FAB form a linear pair.
∴ ∠FAB + ∠FAG = 180°
⇒ 120° + ∠FAG = 180°
⇒ ∠FAG = 180° - 120° = 60°.
Hence, ∠FAG = 60°.
(b) Each interior angle of regular hexagon = 120°.
Hence, ∠BCD = 120°.
(c) In triangle DEF,
⇒ ∠DEF = 120° (Each interior angle of a regular hexagon equals to 120°)
⇒ DE = EF (Sides of a regular hexagon)
⇒ ∠EDF = ∠EFD = a (let) (Angles opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠DEF + ∠EDF + ∠EFD = 180°
⇒ 120° + a + a = 180°
⇒ 2a = 180° - 120°
⇒ 2a = 60°
⇒ a = = 30°
⇒ ∠EFD = 30°.
By alternate segment theorem,
The angle between a tangent to a circle and a chord drawn from the point of contact is equal to the angle subtended by that chord in the alternate segment of the circle.
∴ ∠PDE = ∠EFD = 30°.
Hence, ∠PDE = 30°.
Answered By
24 Likes
Related Questions
Construct a triangle ABC such that AB = 7 cm, BC = 6 cm and CA = 5 cm.
(a) Draw the locus of the points such that
(i) it is equidistant from BC and BA.
(ii) it is equidistant from points A and B.
(b) Mark P where the loci (i) and (ii) meet, measure and write length of PA.
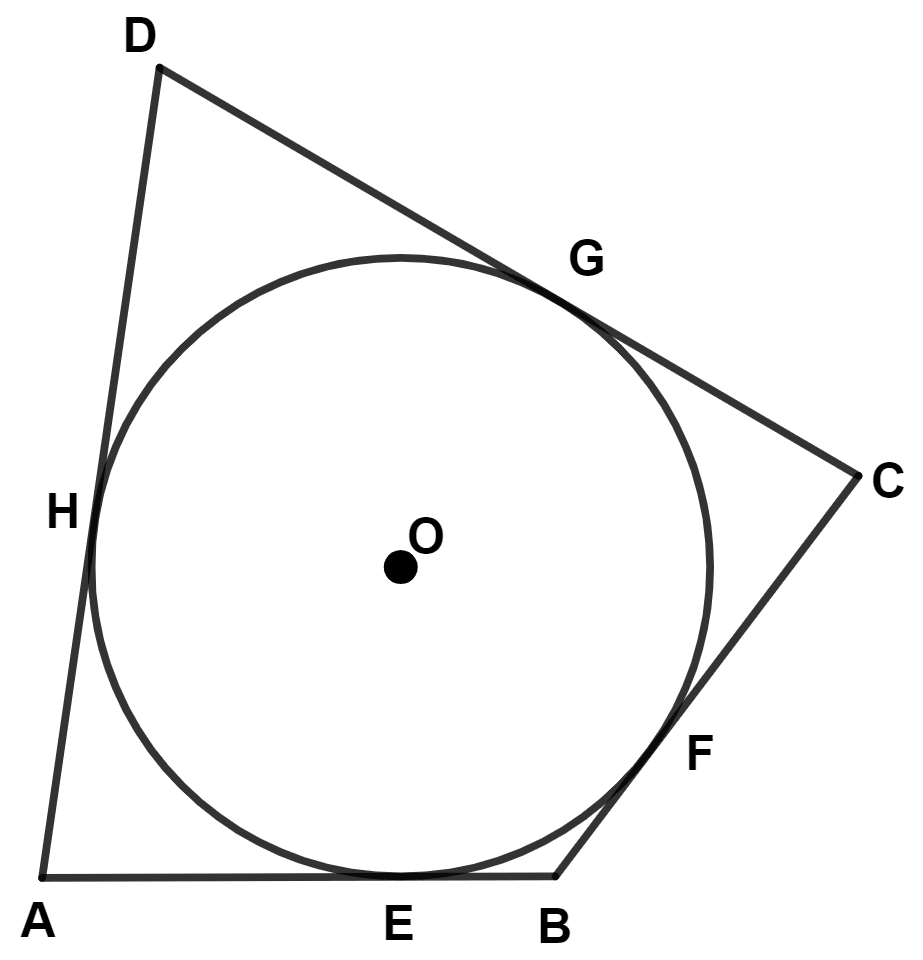
In the given figure O is the centre of the circle. ABCD is a quadrilateral where sides AB, BC, CD and DA touch the circle at E, F, G and H respectively. If AB = 15 cm, BC = 18 cm and AD = 24 cm, find the length of CD.
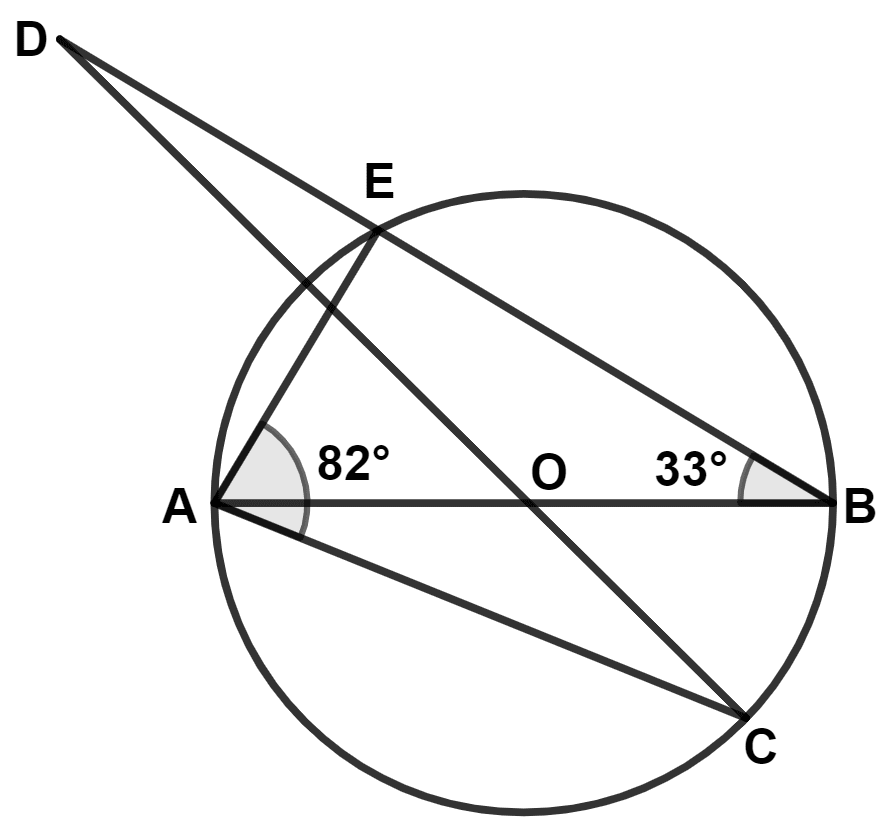
AB and CD intersect at the center O of the circle given in the above diagram. If ∠EBA = 33° and ∠EAC = 82°, find
(a) ∠BAE
(b) ∠BOC
(c) ∠ODB
A famous sweet shop “Madanlal Sweets” sells tinned rasgullas. The tin container is cylindrical in shape with diameter 14 cm, height 16 cm, and it can hold 20 spherical rasgullas of diameter 6 cm and sweetened liquid such that the can is filled and then sealed. Find out how much sweetened liquid the can contains. Take π = 3.14.