Mathematics
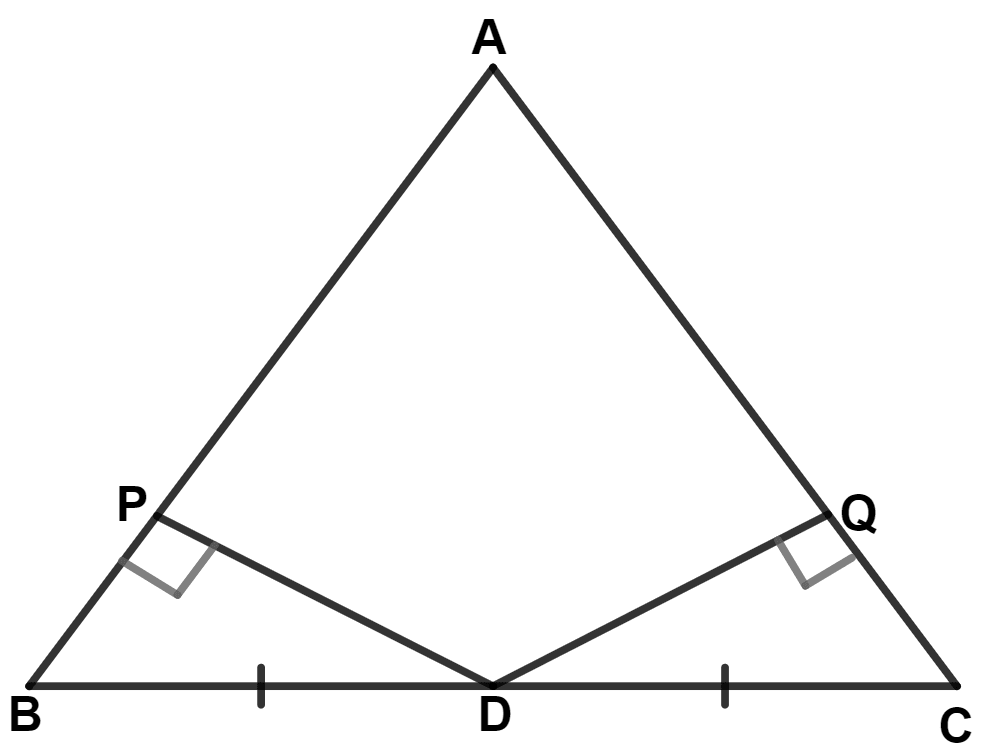
In the given figure, AB = AC. Prove that :
(i) DP = DQ
(ii) AP = AQ
(iii) AD bisects angle A
Answer
(i) In △ ABC,
⇒ AB = AC (Given)
∴ ∠B = ∠C (Angles opposite to equal sides are equal)
In △ PDB and △ QDC,
⇒ ∠P = ∠Q (Both equal to 90°)
⇒ ∠B = ∠C (Proved above)
⇒ BD = CD (Given)
∴ △ PDB ≅ △ QDC (By A.A.S. axiom)
We know that,
Corresponding sides of congruent triangle are equal.
∴ DP = DQ
Hence, proved that DP = DQ.
(ii) Since, △ PDB ≅ △ QDC
∴ BP = QC = y (let) [By C.P.C.T.C.]
⇒ AB = AC = x (let)
From figure,
⇒ AP = AB - BP = x - y
⇒ AQ = AC - QC = x - y
∴ AP = AQ.
Hence, proved that AP = AQ.
(iii) Join AD.
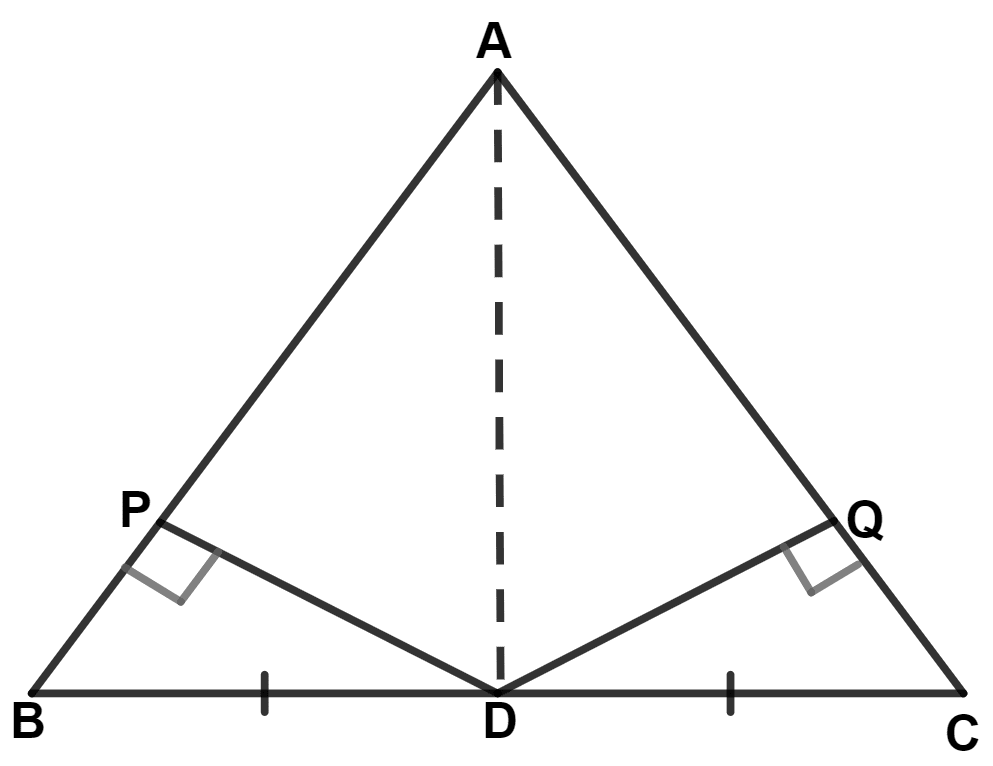
In △ ABD and △ ACD,
⇒ AB = AC (Proved above)
⇒ BD = CD (Given)
⇒ AD = AD (Common side)
∴ △ ABD ≅ △ ACD (By S.S.S. axiom)
We know that,
Corresponding sides of congruent triangle are equal.
∴ ∠BAD = ∠CAD.
Hence, proved that AD bisects angle A.
Related Questions
ABCD is a rectangle. X and Y are points on sides AD and BC respectively such that AX = BY, then :
AY ≠ BX
△ ABX ≅ △ BYA
△ ABX ≅ △ AYB
△ ABX ≅ △ BAY
In the given figure, P is mid-point of side AD of rectangle ABCD; then :
∠PBC = ∠PBA
∠PBC = ∠PCB
∠BPA = ∠BPC
∠PBC = ∠BPA
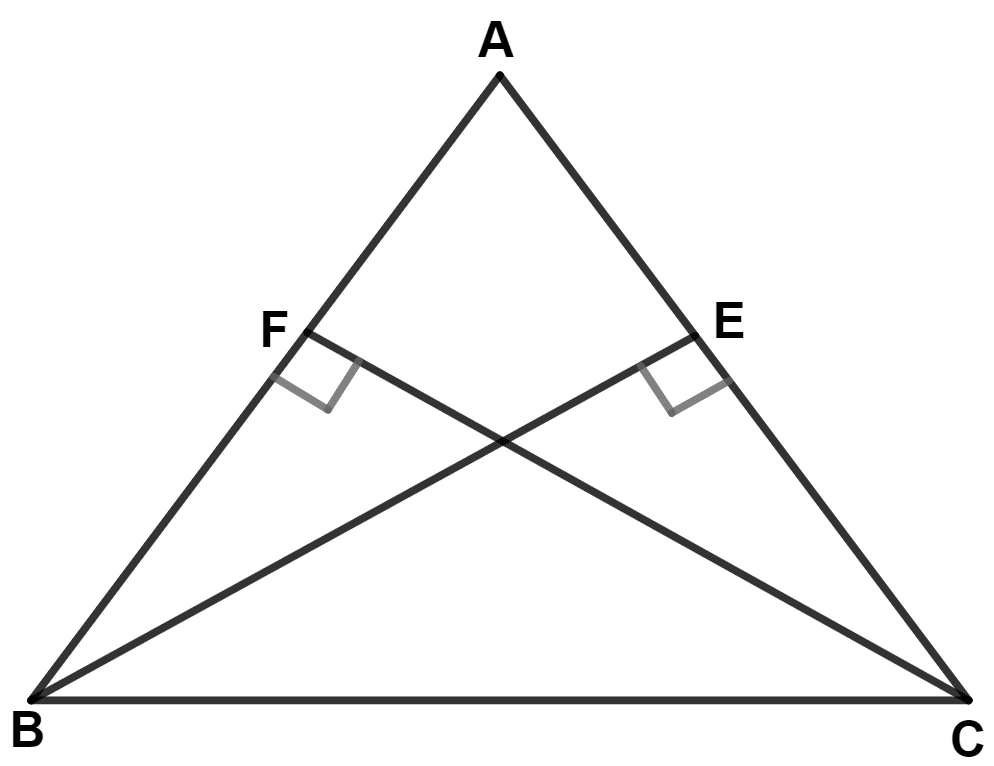
In triangle ABC, AB = AC; BE ⊥ AC and CF ⊥ AB. Prove that :
(i) BE = CF
(ii) AF = AE
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD. Prove that : ∠BCD = 90°.