Mathematics
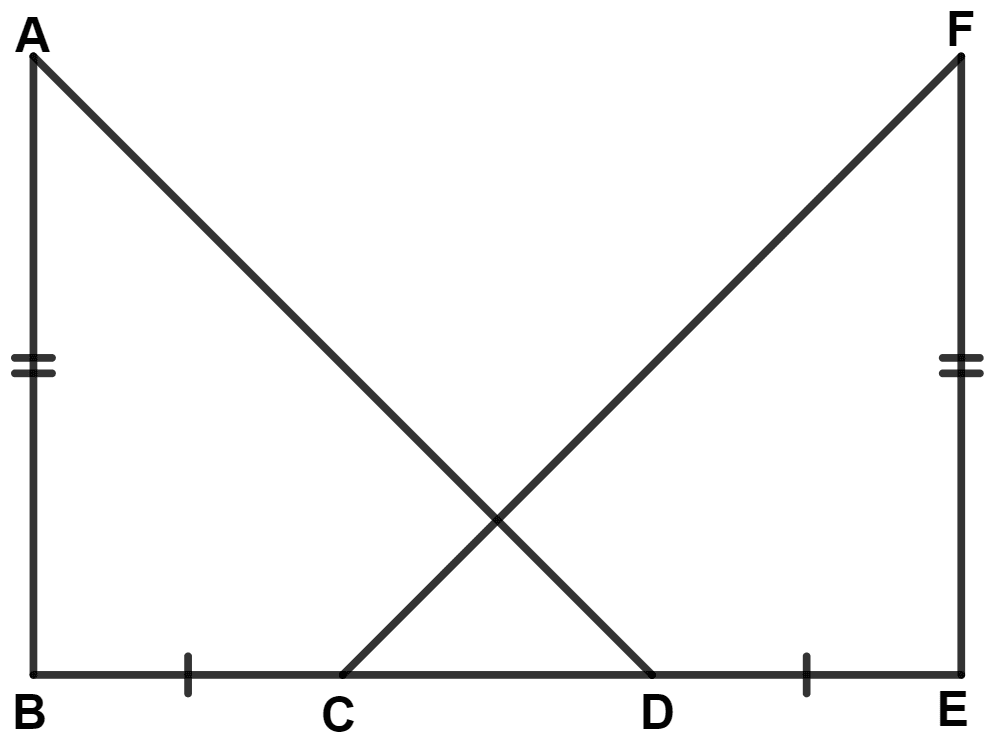
In the given figure, AB ⊥ BE, EF ⊥ BE, AB = EF and BC = DE, then :
△ ABD ≅ △ EFC
△ ABD ≅ △ FEC
△ ABD ≅ △ ECF
△ ABD ≅ △ CEF
Triangles
11 Likes
Answer
Since, AB ⊥ BE and EF ⊥ BE,
∴ ∠ABE = 90° and ∠FEB = 90°.
From figure,
⇒ ∠ABD = ∠ABE = 90°
⇒ ∠FEC = ∠FEB = 90°
Given,
⇒ BC = DE
⇒ BC + CD = CD + DE
⇒ BD = CE.
In △ ABD and △ FEC,
⇒ AB = FE (Given)
⇒ BD = CE (Proved above)
⇒ ∠ABD = ∠FEC (Both equal to 90°)
∴ △ ABD ≅ △ FEC (By S.A.S. axiom)
Hence, Option 2 is the correct option.
Answered By
7 Likes
Related Questions
In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.
In triangle ABC; ∠A = 60°, ∠C = 40° and bisector of angle ABC meets side AC at point P. Show that BP = CP.
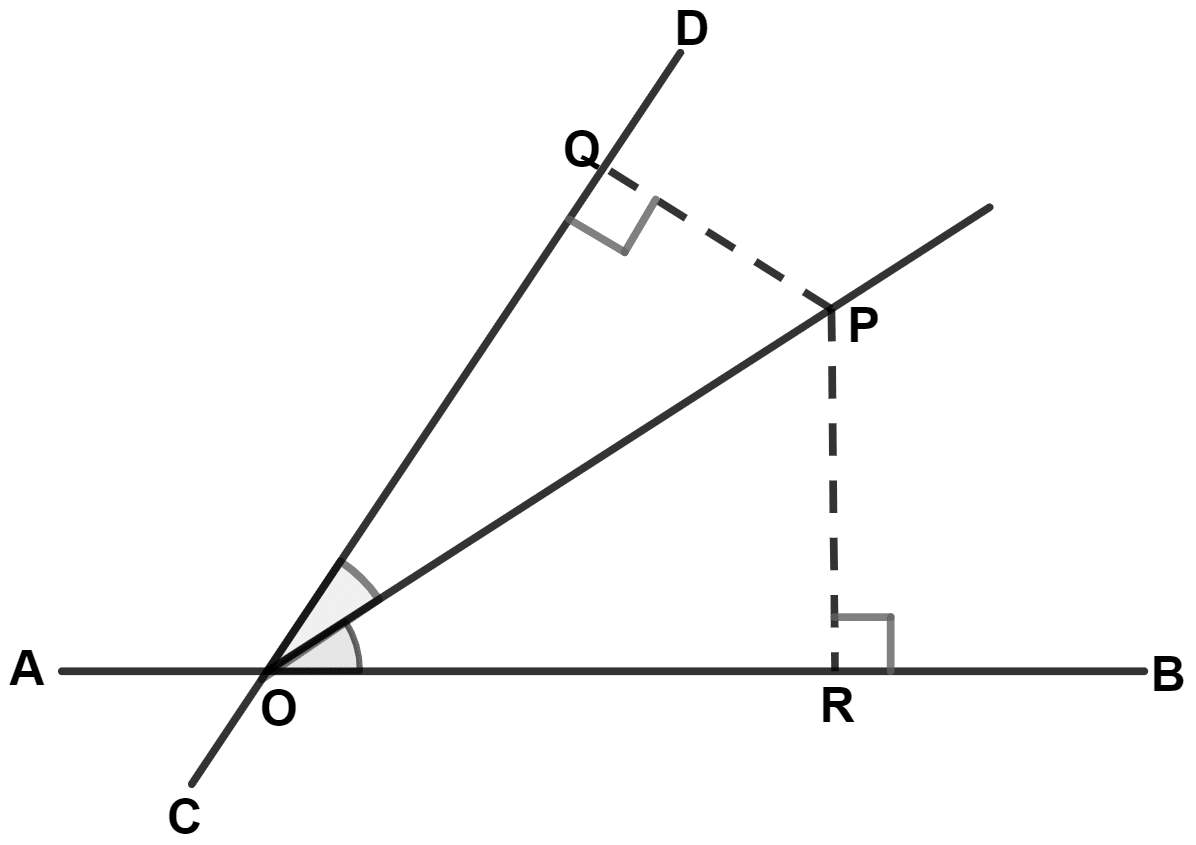
From the adjoining figure, we find :
OP = OR
OP = OQ
PQ = PR
PR ≠ PQ
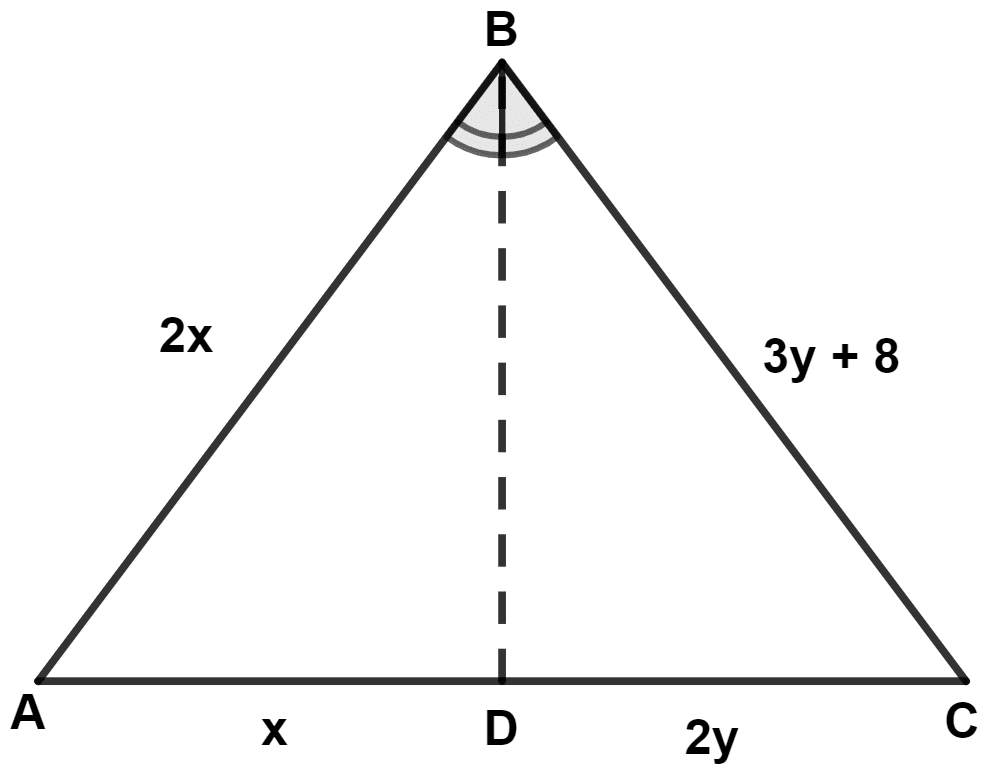
From the given figure, if ∠A = ∠C, we get :
x = 8, y = 16
x = -8, y = 16
x = 16, y = -8
x = 16, y = 8