Mathematics
In the given figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that △ABC ~ △EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of △BED = 9 cm2. Calculate the :
(i) length of AB
(ii) area of △ABC

Similarity
18 Likes
Answer
(i) In △ABC and △EBD,
⇒ ∠EDB = ∠ACB [Given]
⇒ ∠DBE = ∠ABC [Common]
∴ △ABC ~ △EBD
From figure,
⇒ BC = BE + EC = 6 + 4 = 10 cm.
Since, corresponding sides of similar triangles are proportional to each other.
Hence, length of AB = 12 cm.
(ii) We know that,
Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.
Hence, area of ∆ABC = 36 cm2.
Answered By
10 Likes
Related Questions
Two isosceles triangles have equal vertical angles. Show that the triangles are similar.
If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
In △ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find :
(i) area △APO : area △ABC
(ii) area △APO : area △CQO.

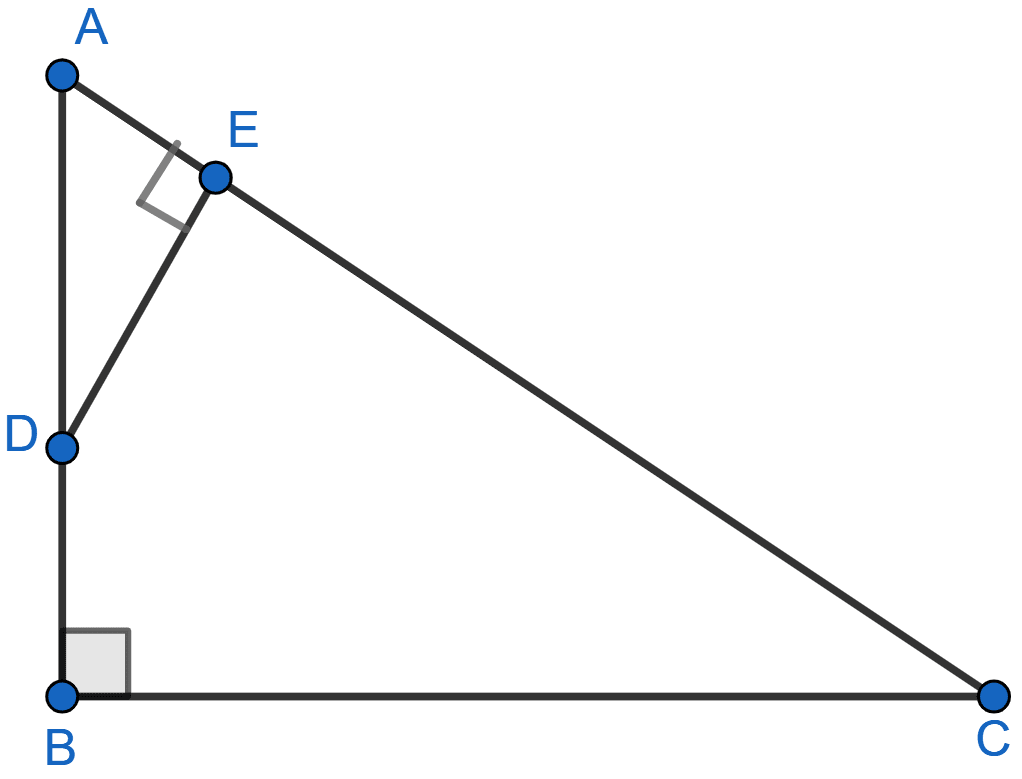
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
(i) Prove that : △ADB ~ △CDA.
(ii) If BD = 18 cm and CD = 8 cm, find AD.
(iii) Find the ratio of the area of △ADB is to area of △CDA.
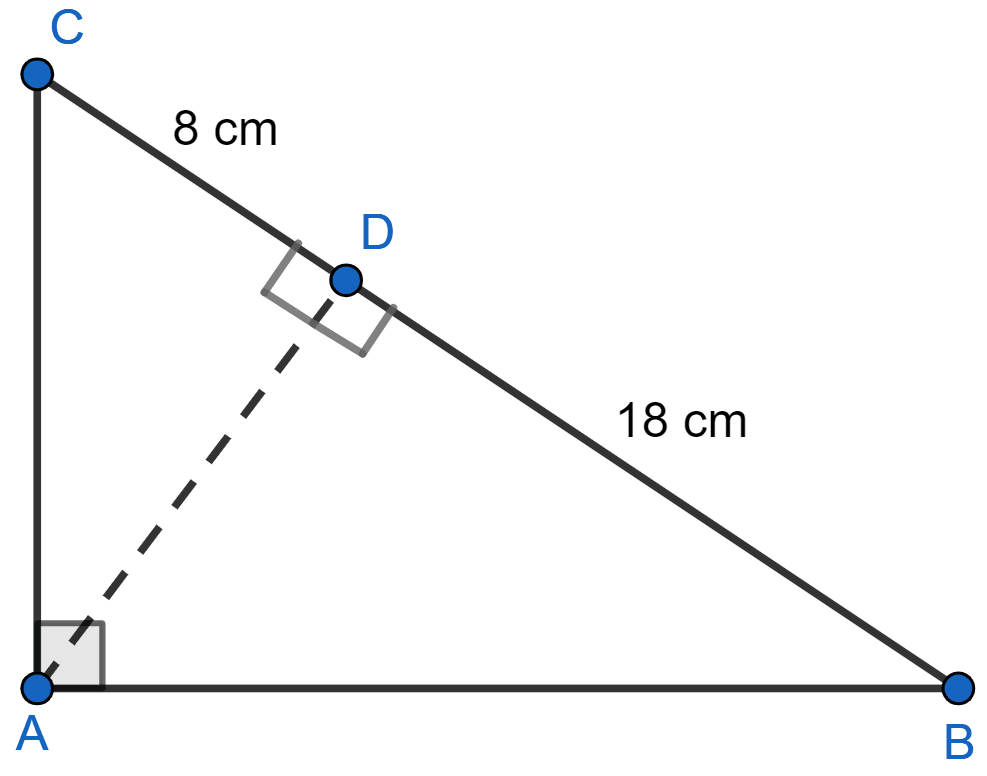
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
(i) △ADE ~ △ACB
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of △ADE : area of quadrilateral BCED.