Mathematics
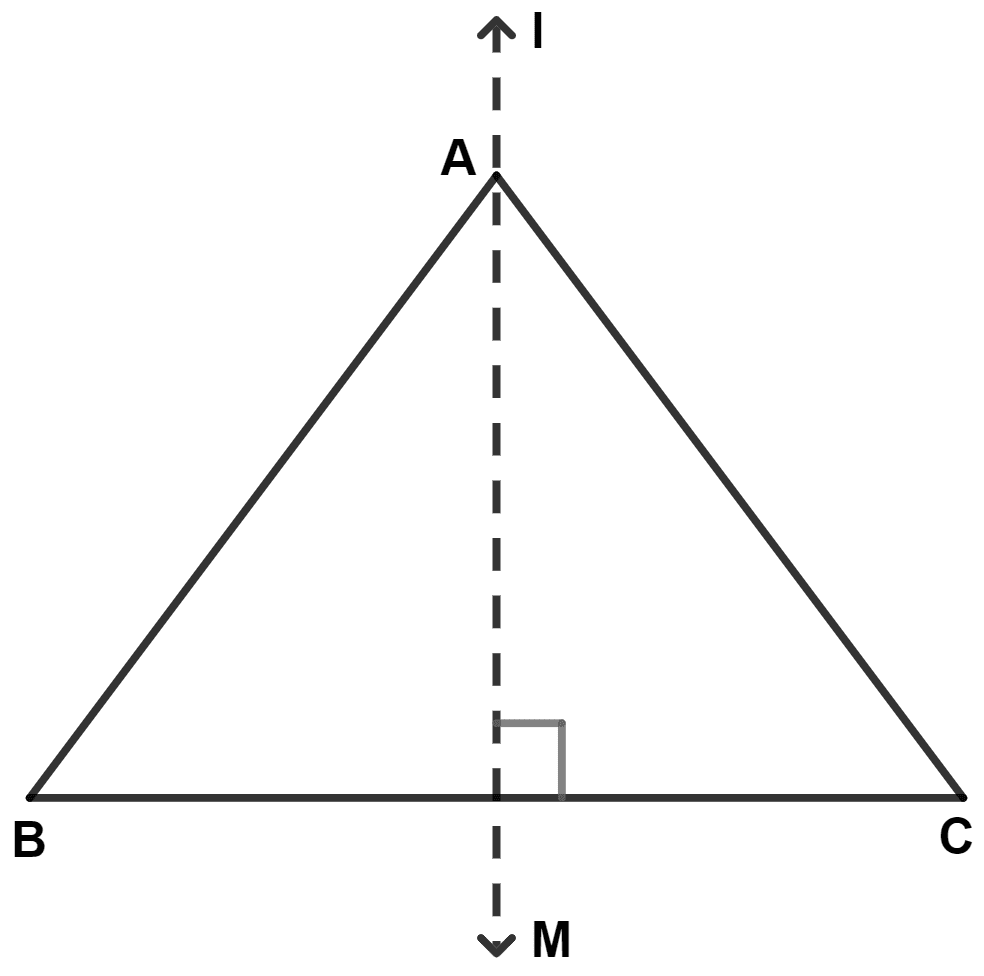
In the given figure, AM is the perpendicular bisector of BC. Then :
AB = AM
AC = BM
AB ≠ AC
AM bisects ∠BAC
Triangles
34 Likes
Answer
From figure,
In △ ABM and △ ACM,
⇒ ∠AMB = ∠AMC (Both equal to 90°)
⇒ BM = MC (Since, AM is perpendicular bisector of BC)
⇒ AM = AM (Common side)
∴ △ ABM ≅ △ ACM (By S.A.S. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ ∠BAM = ∠CAM (By C.P.C.T.C.)
∴ AM bisects ∠BAC.
Hence, Option 4 is the correct option.
Answered By
21 Likes
Related Questions
If △ ABC ≅ △ PQR, then
AC = PR
AC = PQ
BC = PR
BC = PQ
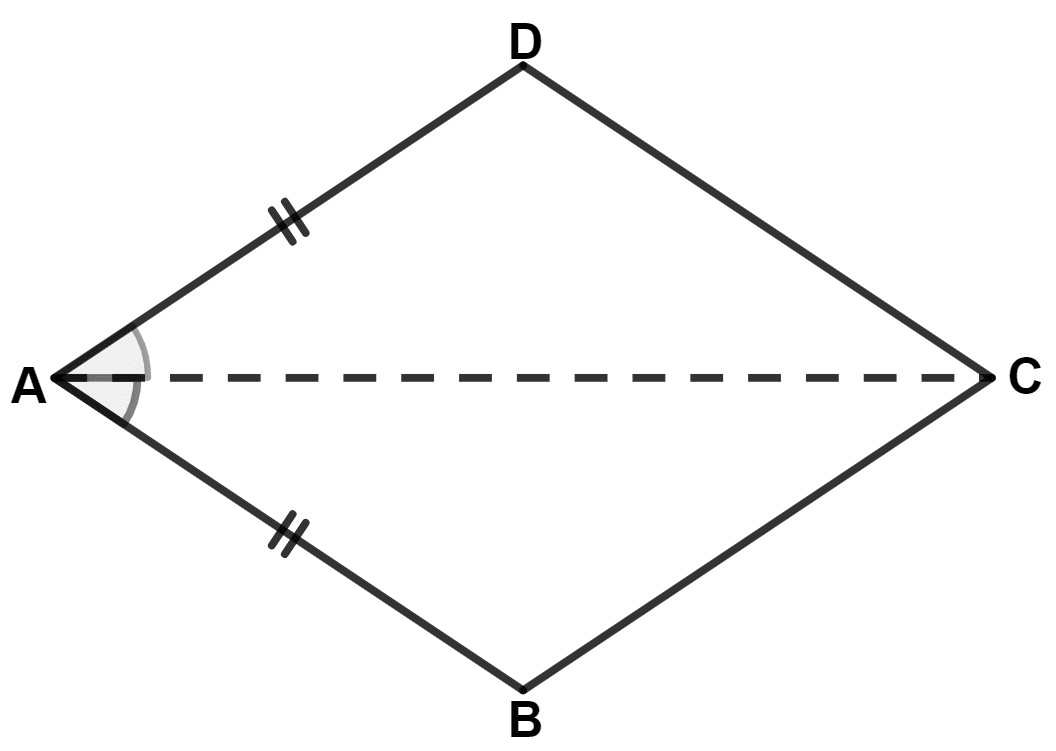
Which of the following will hold true for the given figure :
AD = DC
CD = CB
∠ACD ≠ ∠ACB
∠B ≠ ∠D
Which of the following is true for the given figure:
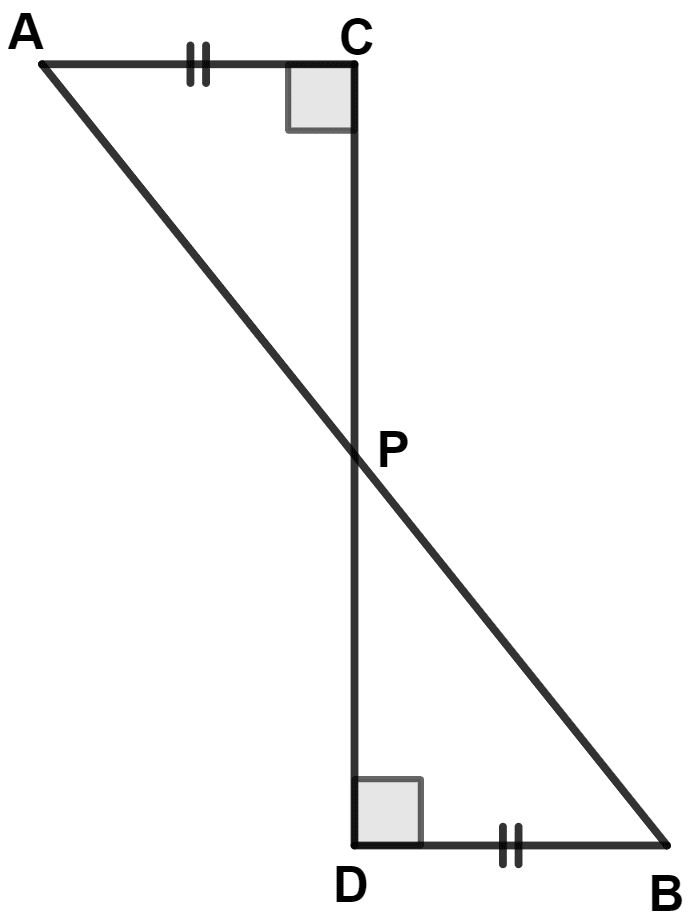
ΔAPC ≅ ΔBPD
CP = DP
AB and CD bisect each other
all of the above are true.
In the following figure, ∠BAD = ∠EAC, BD = EC and ∠B = ∠E, then :
△ ABD ≇ △ AEC
△ ABC ≅ △ AED
△ ABC ≇ △ AED
△ ABD ≅ △ ADE