Mathematics
In the given figure, arc AB and arc BC are equal in length.
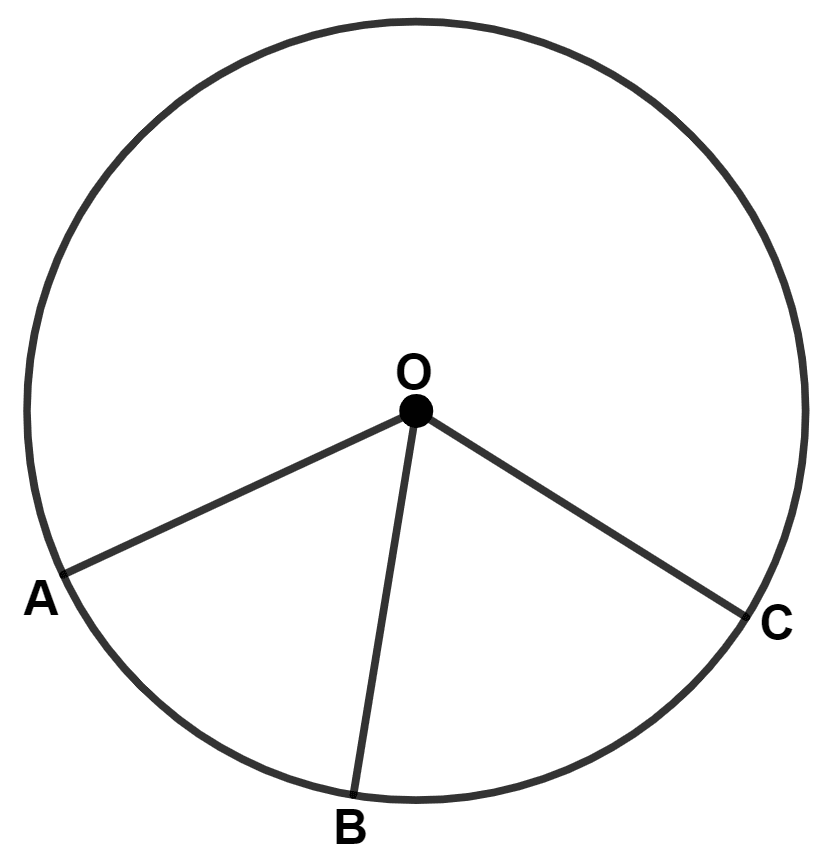
If ∠AOB = 48°, find :
(i) ∠BOC
(ii) ∠OBC
(iii) ∠AOC
(iv) ∠OAC
Circles
45 Likes
Answer
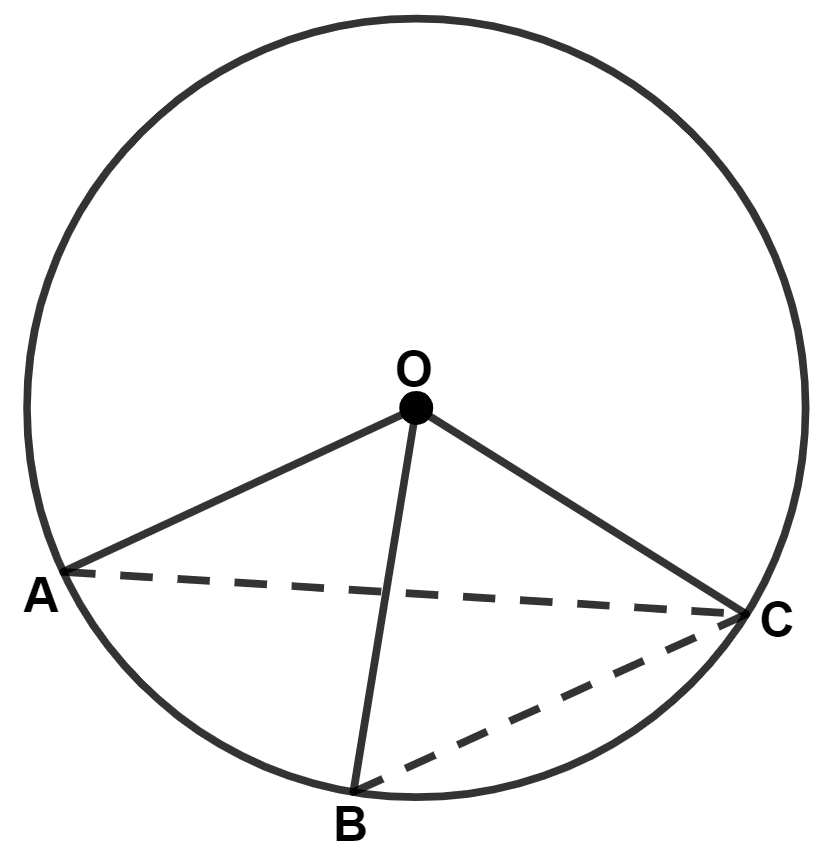
(i) We know that,
If two arcs are of a circle are equal, they subtend equal angles at the center.
∴ ∠BOC = ∠AOB = 48°.
Hence, ∠BOC = 48°.
(ii) Join BC.
In △ OBC,
⇒ OC = OB (Radius of same circle)
⇒ ∠OBC = ∠OCB = y (let) [Angle opposite to equal sides are equal]
By angle sum property of triangle,
⇒ ∠OBC + ∠OCB + ∠BOC = 180°
⇒ y + y + 48° = 180°
⇒ 2y + 48° = 180°
⇒ 2y = 180° - 48°
⇒ 2y = 132°
⇒ y =
⇒ y = 66°
⇒ ∠OBC = 66°.
Hence, ∠OBC = 66°.
(iii) From figure,
⇒ ∠AOC = ∠AOB + ∠BOC = 48° + 48° = 96°.
Hence, ∠AOC = 96°.
(iv) Join AC.
In △ AOC,
⇒ OC = OA (Radius of same circle)
⇒ ∠OAC = ∠OCA = x (let) [Angle opposite to equal sides are equal]
By angle sum property of triangle,
⇒ ∠OAC + ∠OCA + ∠AOC = 180°
⇒ x + x + 96° = 180°
⇒ 2x + 96° = 180°
⇒ 2x = 180° - 96°
⇒ 2x = 84°
⇒ x =
⇒ x = 42°
⇒ ∠OAC = 42°.
Hence, ∠OAC = 42°.
Answered By
33 Likes
Related Questions
In the given figure, a square is inscribed in a circle with center O. Find :
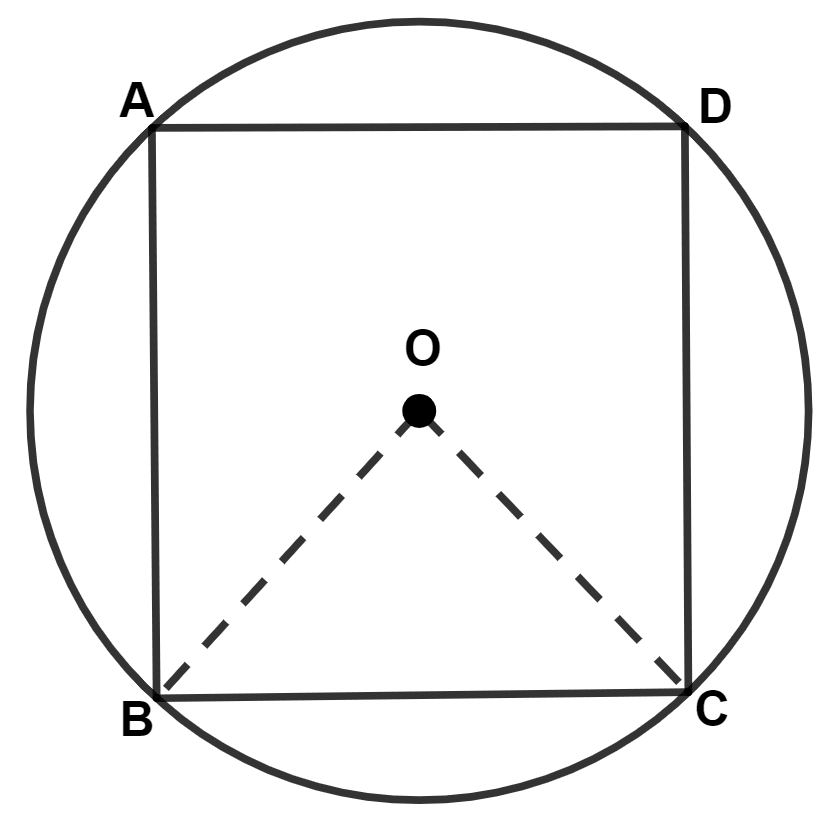
(i) ∠BOC
(ii) ∠OCB
(iii) ∠COD
(iv) ∠BOD
Is BD a diameter of the circle?
In the given figure, AB is a side of a regular pentagon and BC is a side of a regular hexagon.
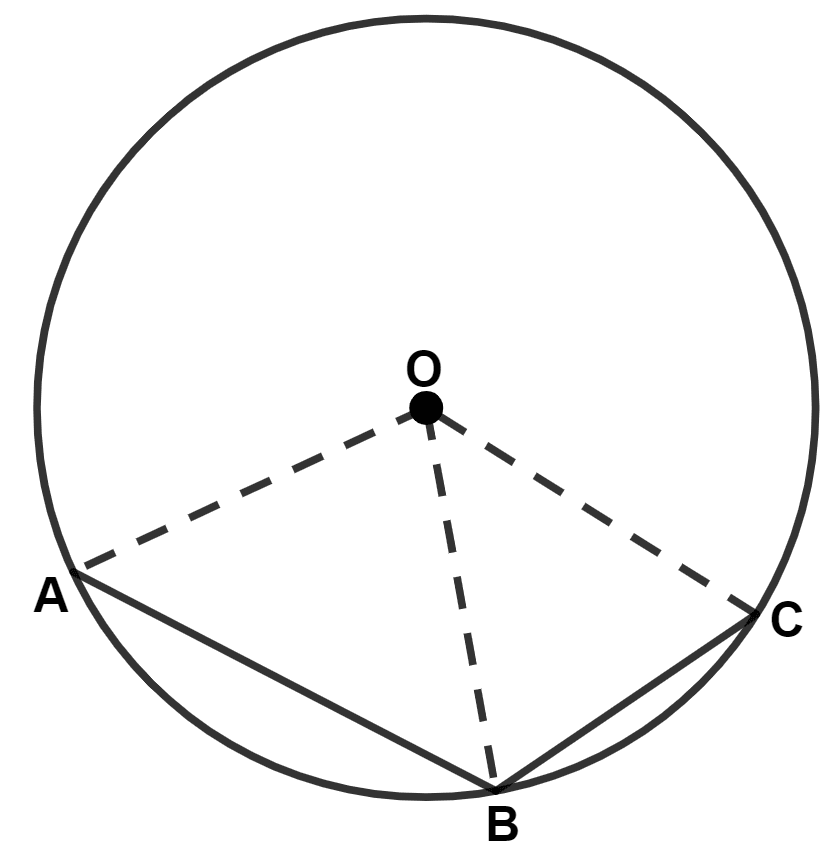
(i) ∠AOB
(ii) ∠BOC
(iii) ∠AOC
(iv) ∠OBA
(v) ∠OBC
(vi) ∠ABC
In the given figure, the lengths of arcs AB and BC are in the ratio 3 : 2.
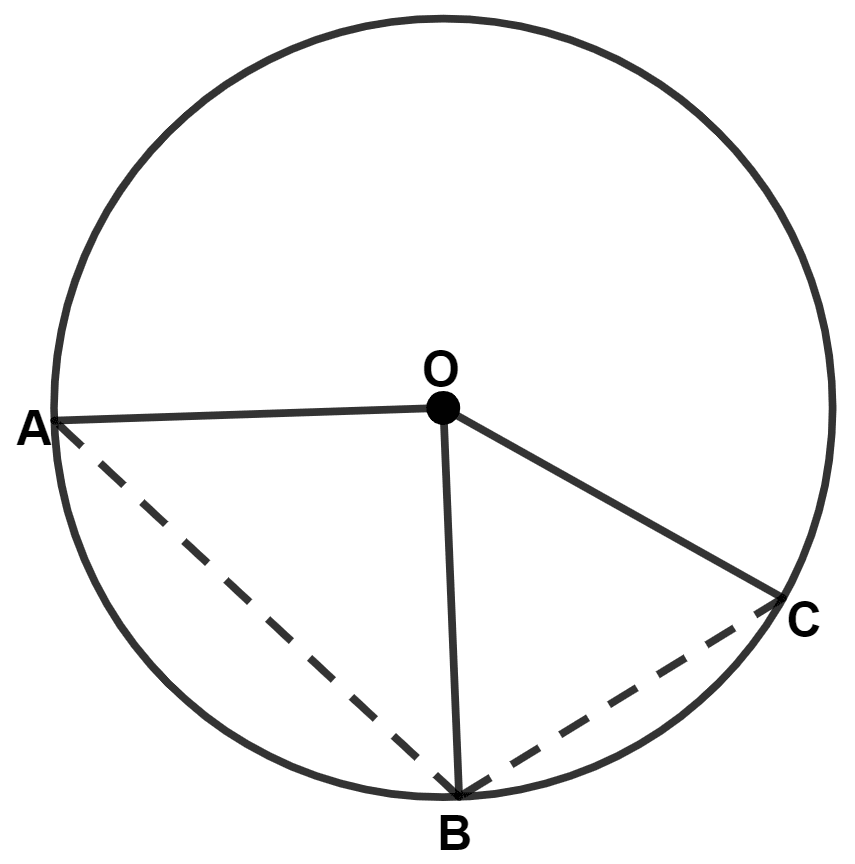
If ∠AOB = 96°, find :
(i) ∠BOC
(ii) ∠ABC
In the given figure, AB = BC = DC and ∠AOB = 50°. Find :
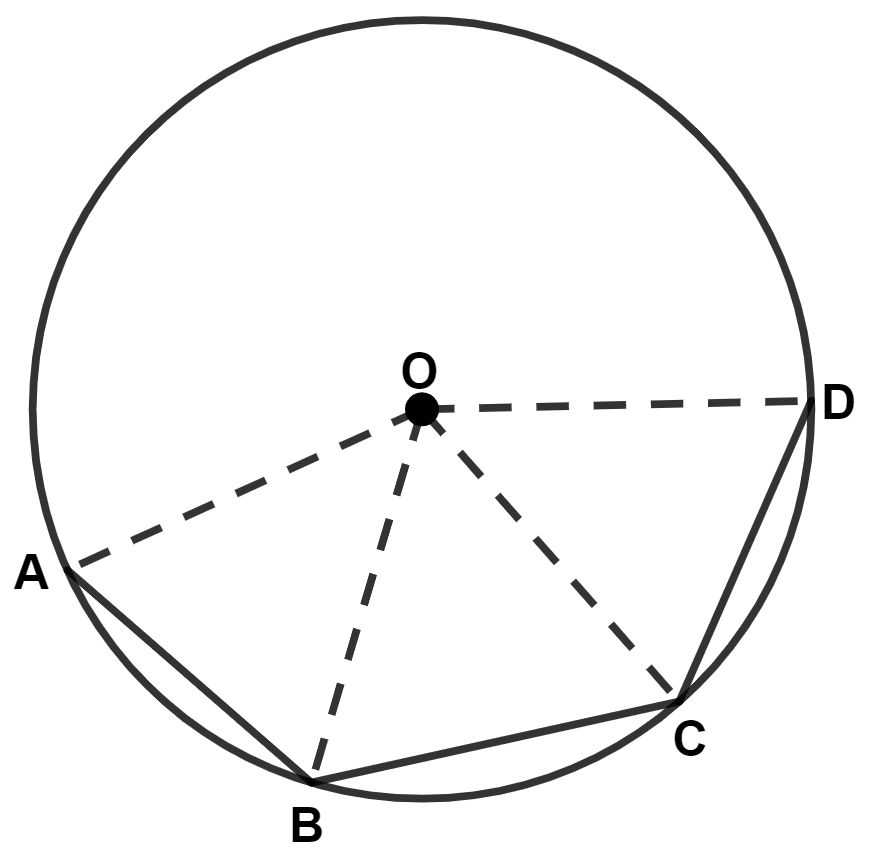
(i) ∠AOC
(ii) ∠AOD
(iii) ∠BOD
(iv) ∠OAC
(v) ∠ODA