KnowledgeBoat Logo
|

Mathematics

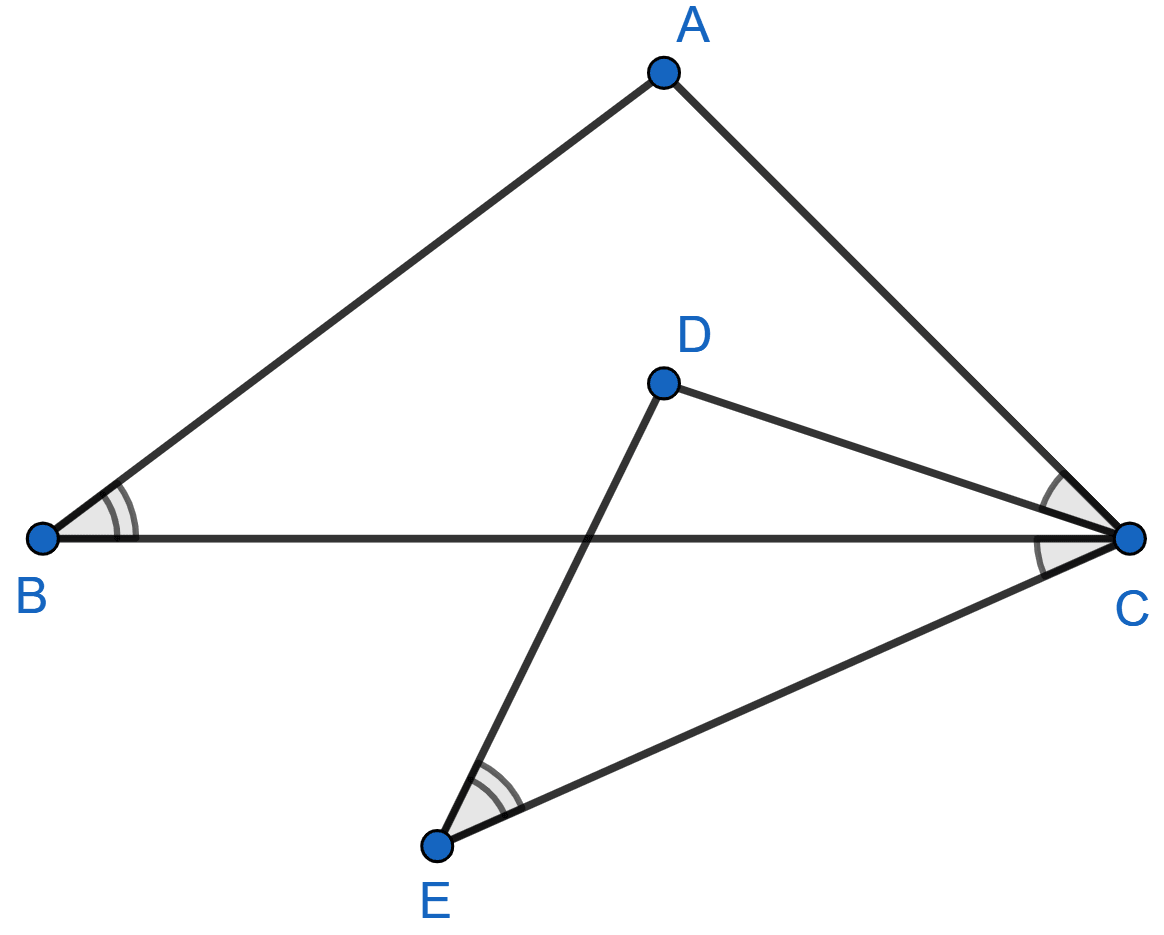
In the given figure,

∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the △ABC and △DEC.

In the figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the △ABC and △DEC. Similarity, Concise Mathematics Solutions ICSE Class 10.

Similarity

25 Likes

Answer

Given,

⇒ ∠ACD = ∠BCE

⇒ ∠ACD + ∠BCD = ∠BCE + ∠BCD

⇒ ∠ACB = ∠DCE

Also, ∠B = ∠E

∴ △ABC ~ △DEC [By AA]

We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

∴Area of △ABCArea of △DEC=AB2DE2=(10.47.8)2=(43)2=169.\therefore \dfrac{\text{Area of △ABC}}{\text{Area of △DEC}} = \dfrac{AB^2}{DE^2}\\[1em] = \Big(\dfrac{10.4}{7.8}\Big)^2 = \Big(\dfrac{4}{3}\Big)^2 \\[1em] = \dfrac{16}{9}.

Hence, ratio between areas of the △ABC and △DEC = 16 : 9.

Answered By

15 Likes

Related Questions