Mathematics
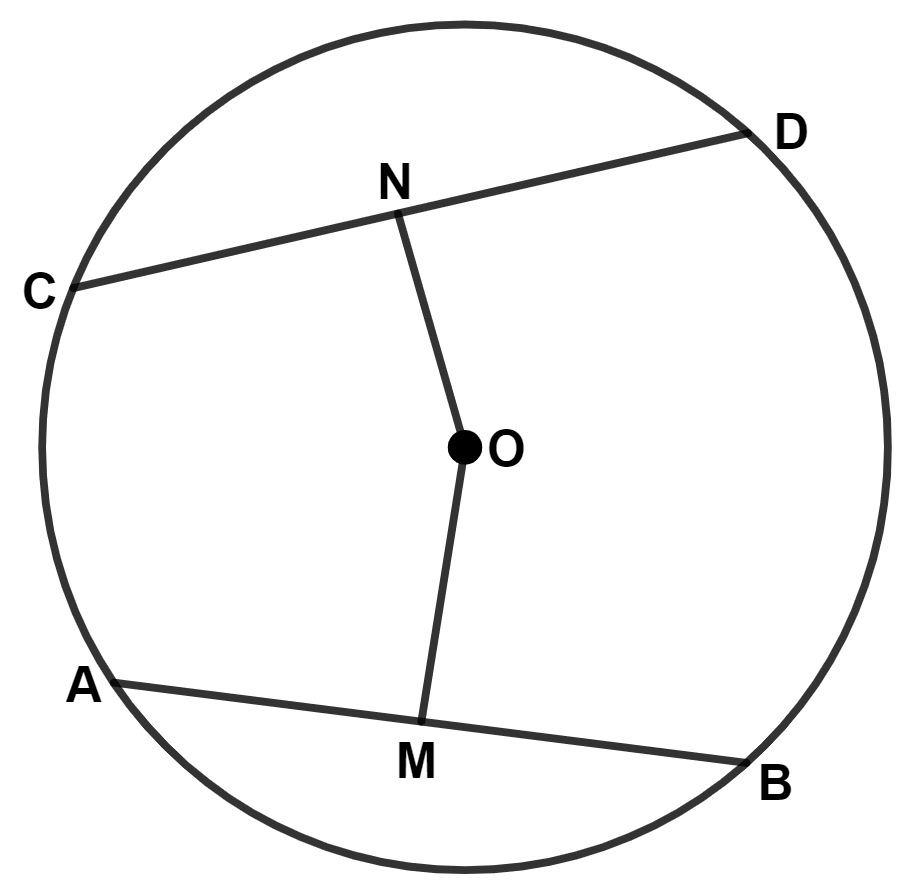
In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) the radius of the circle
(ii) length of chord CD.
Circles
8 Likes
Answer
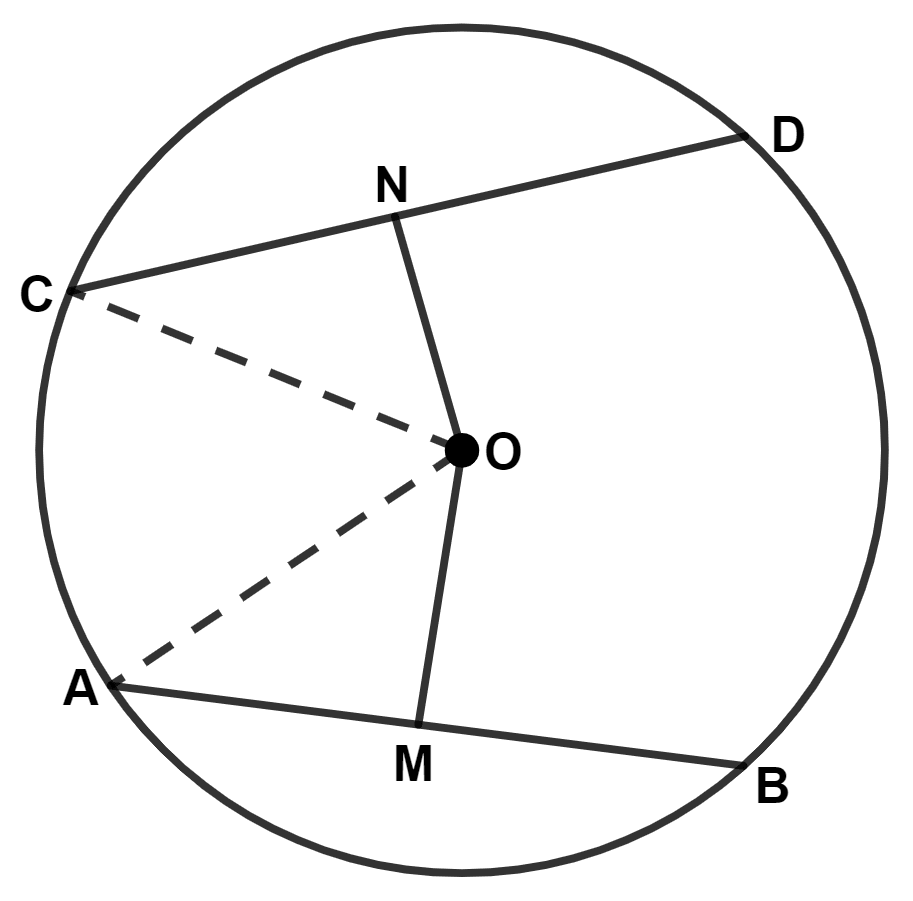
(i) Join OA.
We know that,
Perpendicular from center to chord, bisects the chord.
As, OM ⊥ AB
∴ AM = = 12 cm.
In △ OAM,
By pythagoras theorem,
⇒ Hypotenuse2 = Perpendicular2 + Base2
⇒ OA2 = OM2 + AM2
⇒ OA2 = 52 + 122
⇒ OA2 = 25 + 144
⇒ OA2 = 169
⇒ OA = = 13 cm.
Hence the radius of circle = 13 cm.
(ii) We know that,
Perpendicular from center of the circle to chord, bisects the chord.
As, ON ⊥ CD
∴ CN =
⇒ CD = 2CN ………….(1)
Join OC.
In △ OCN,
By pythagoras theorem,
⇒ Hypotenuse2 = Perpendicular2 + Base2
⇒ OC2 = ON2 + NC2
⇒ 132 = 122 + CN2
⇒ CN2 = 132 - 122
⇒ CN2 = 169 - 144
⇒ CN2 = 25
⇒ CN = = 5 cm.
Substituting value of CN in equation (1), we get :
⇒ CD = 2 × 5 = 10 cm.
Hence, length of chord CD = 10 cm.
Answered By
6 Likes
Related Questions
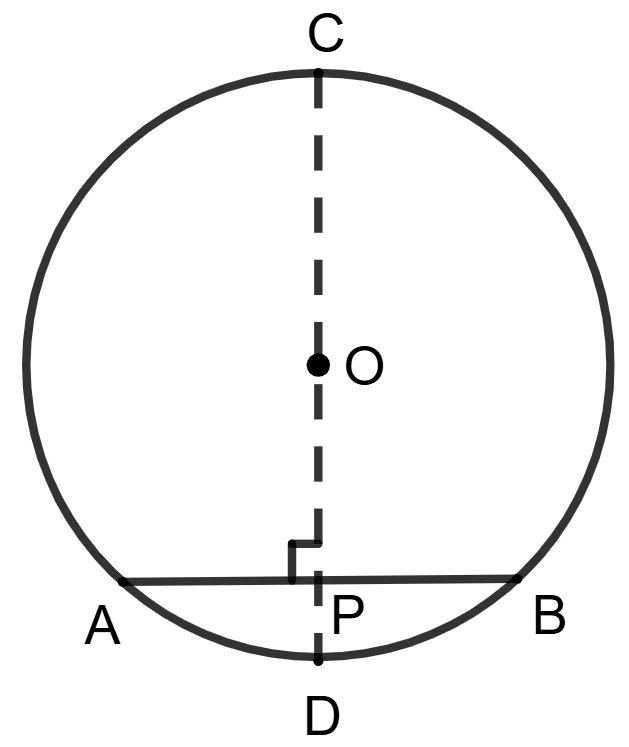
Assertion (A): In the given figure, chord AB = 8 cm, diameter CD = 20 cm, then length of OP = 10 cm.
Reason (R): OP =
and CP = OC + OP
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
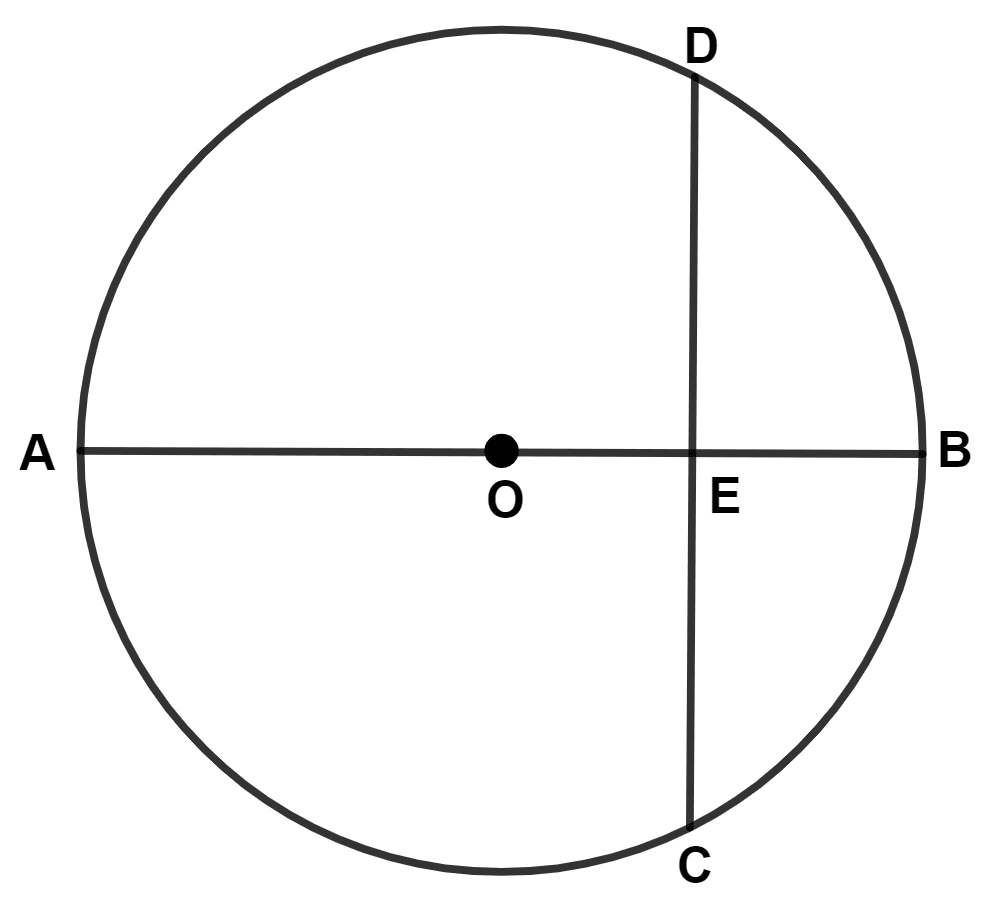
The figure, given below, shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm, find the radius of the circle.
AB and CD are two equal chords of a circle with center O which intersect each other at right angle at point P. If OM ⊥ AB and ON ⊥ CD; show that OMPN is a square.
The radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centers.