Mathematics
In the given figure, O is the center of the circle and ABC is an equilateral triangle, then ∠AOB is equal to :
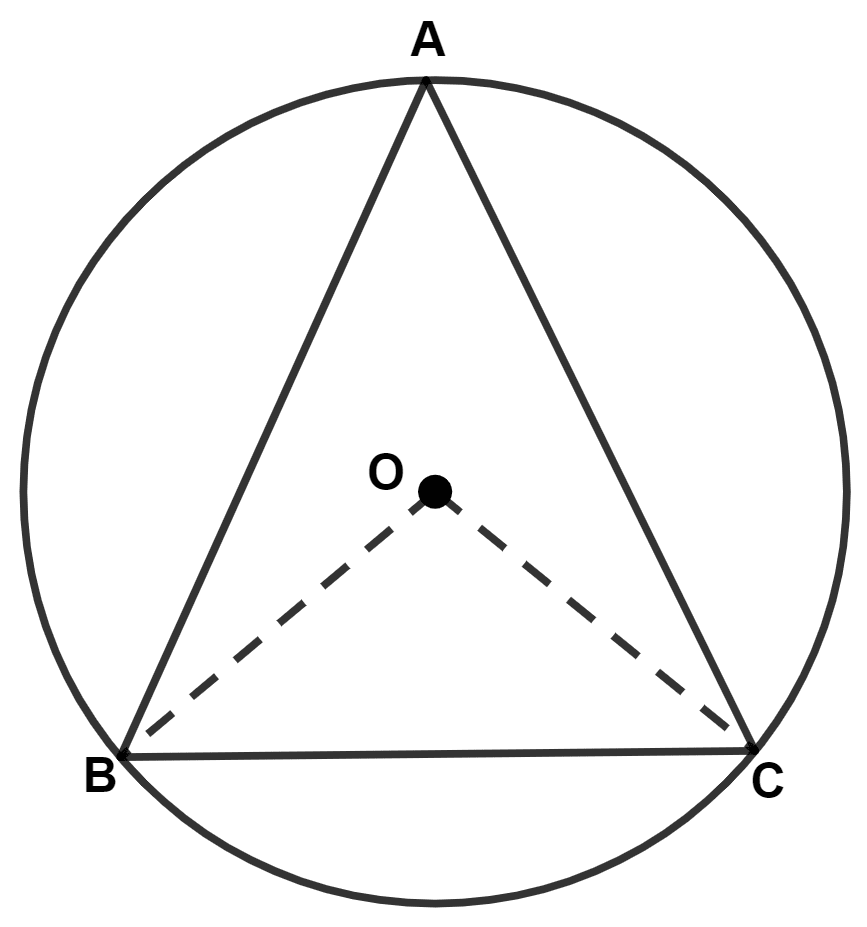
105°
90°
60°
120°
Circles
11 Likes
Answer
Since, ABC is an equilateral triangle.
∴ AB = BC = AC.
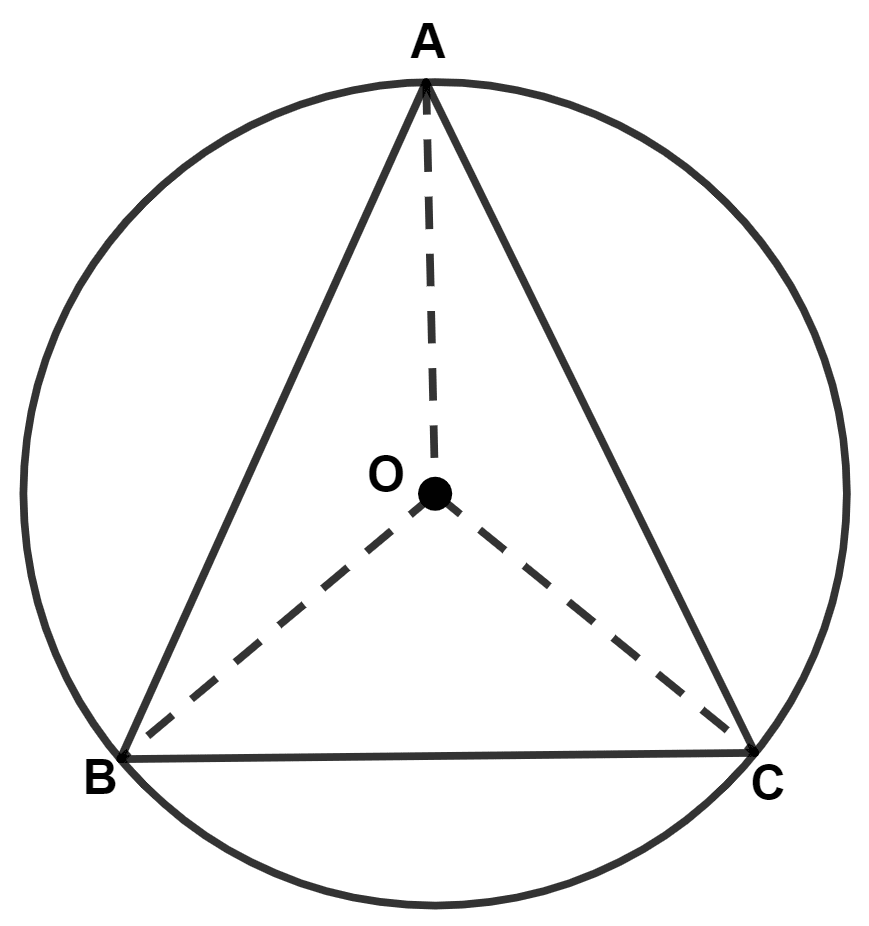
We know that,
Equal chords subtend equal angles at the center.
∴ ∠AOB = ∠BOC = ∠COA = x (let)
We know that,
Angles around a point add to 360 °.
∴ ∠AOB + ∠BOC + ∠COA = 360°
⇒ x + x + x = 360°
⇒ 3x = 360°
⇒ x = = 120°
⇒ ∠AOB = 120°.
Hence, Option 4 is the correct option.
Answered By
8 Likes
Related Questions
In the given figure, O is center of the circle and ∠COD is greater than ∠AOB, then :
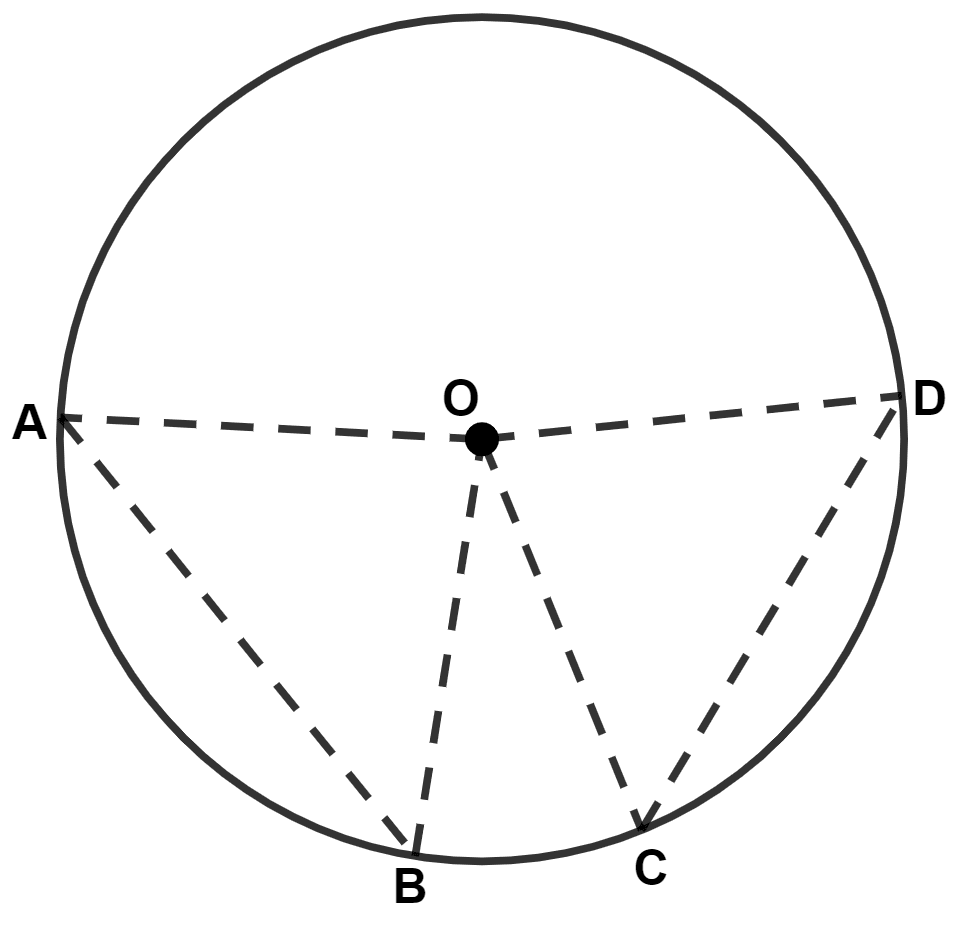
AB > CD
AB < CD
AB = CD
AB + CD = AD
In a circle, O is its center and AB, CD are its two chords. If AB : CD = 3 : 2, then ratio between ∠AOB and ∠COD is :
1 : 1
3 : 2
2 : 5
3 : 5
In the given figure, O is the center of the circle and chord AB : chord CD = 5 : 3. If angle DOC = 60°; then ∠AOB is :
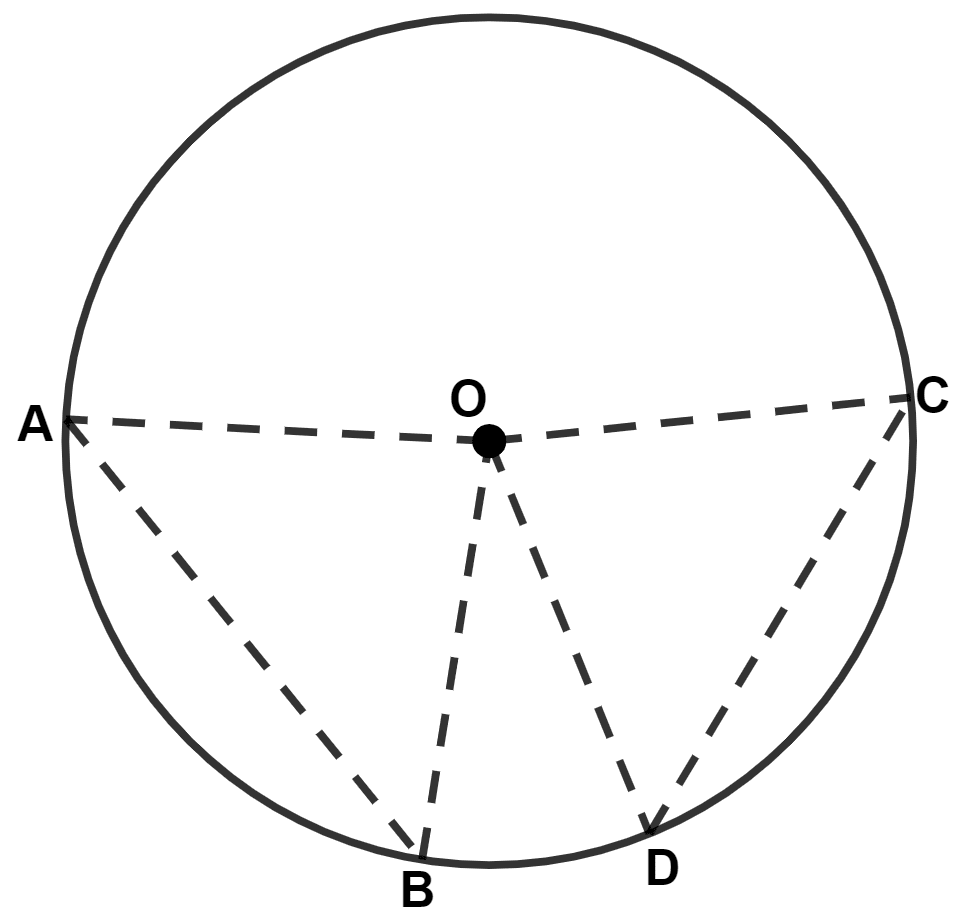
120°
75°
100°
80°
In the given figure, a square is inscribed in a circle with center O. Find :
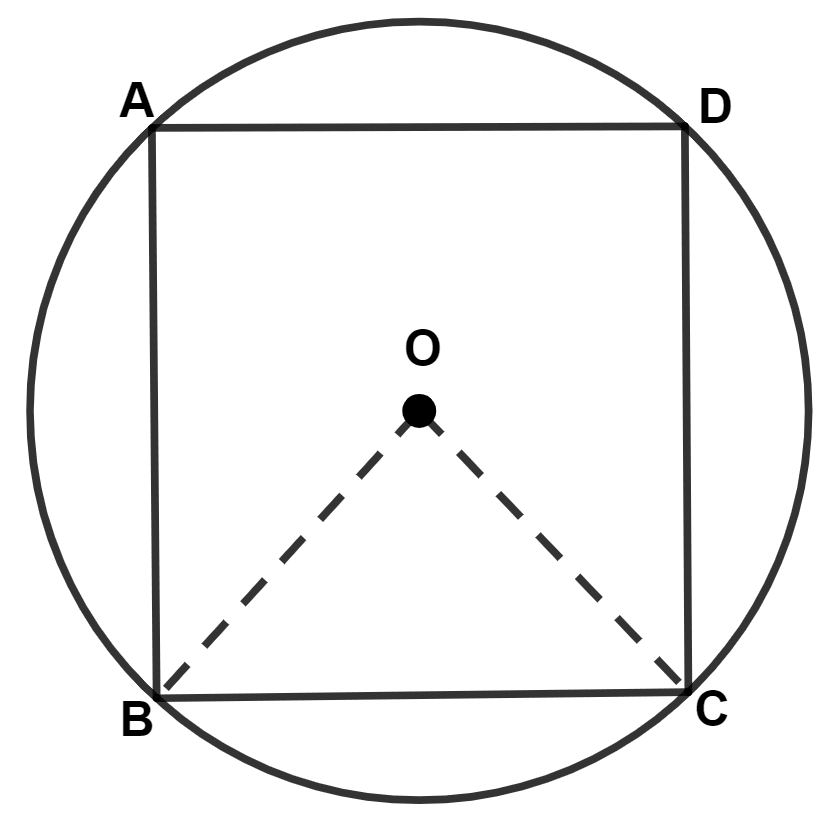
(i) ∠BOC
(ii) ∠OCB
(iii) ∠COD
(iv) ∠BOD
Is BD a diameter of the circle?