Mathematics
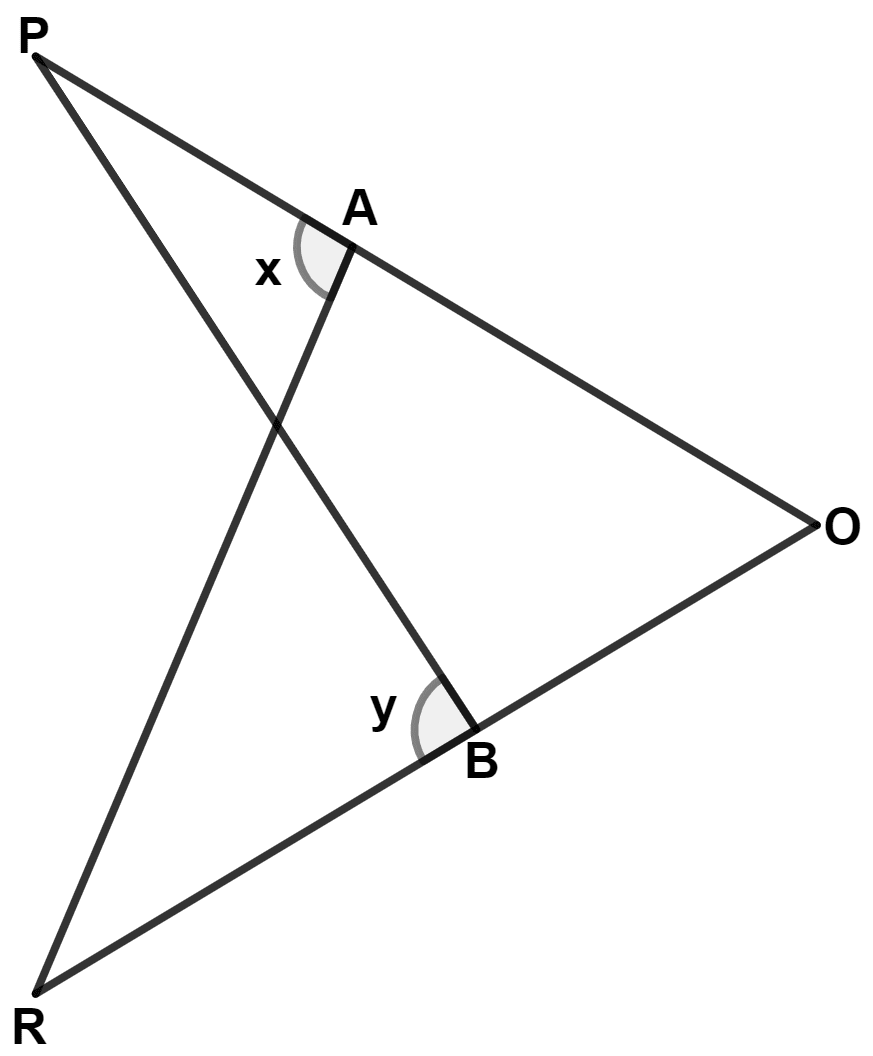
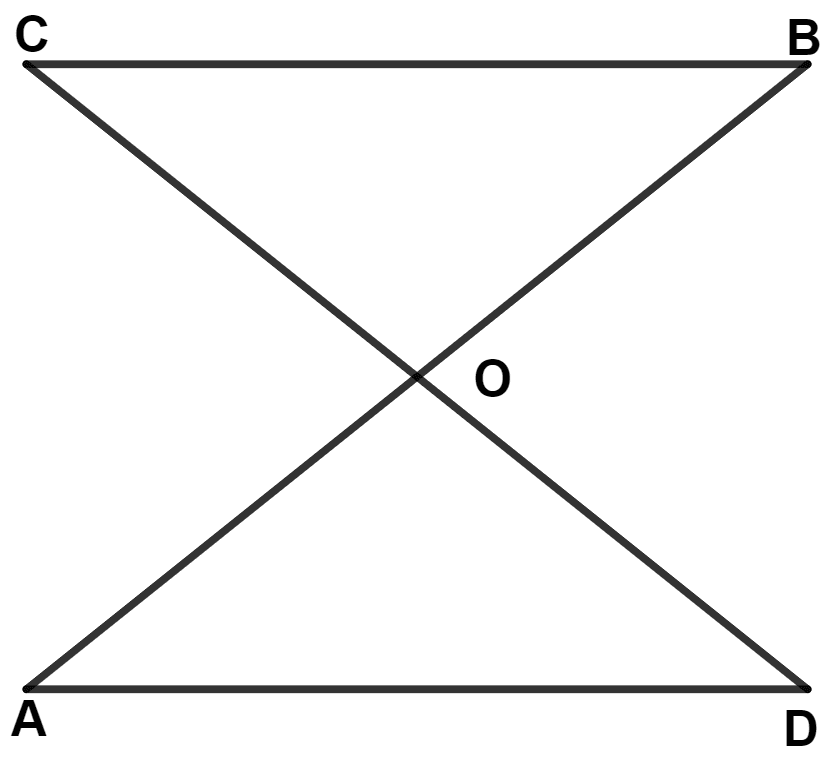
In the given figure, ∠x = ∠y and PO = RO, then :
RB = AO
BO = PA
BP = AR
RB = OB
Triangles
28 Likes
Answer
From figure,
OP is a straight line.
∴ ∠OAR + x = 180°
⇒ ∠OAR = 180° - x
OR is a straight line.
∴ ∠PBO + y = 180°
⇒ ∠PBO = 180° - y
Since, ∠x = ∠y
∴ ∠OAR = ∠PBO
In △ PBO and △ OAR,
⇒ PO = RO (Given)
⇒ ∠PBO = ∠OAR (Proved above)
⇒ ∠O = ∠O (Common angle)
∴ △ PBO ≅ △ OAR (By A.A.S. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ BP = AR.
Hence, Option 3 is the correct option.
Answered By
17 Likes
Related Questions
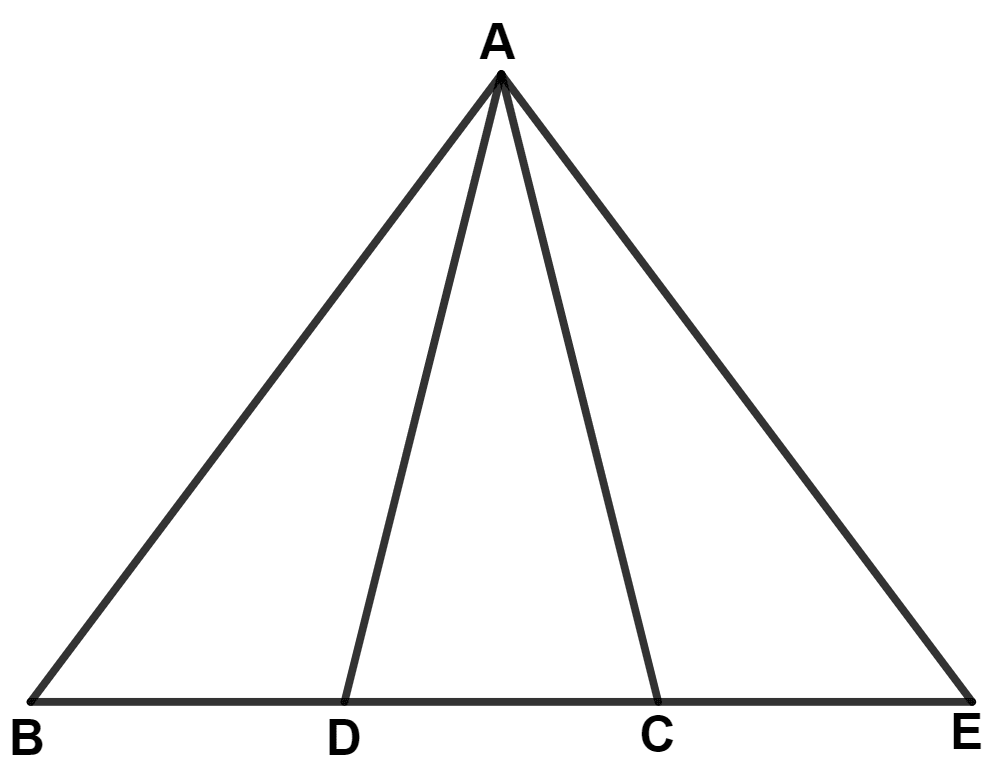
In the following figure, ∠BAD = ∠EAC, BD = EC and ∠B = ∠E, then :
△ ABD ≇ △ AEC
△ ABC ≅ △ AED
△ ABC ≇ △ AED
△ ABD ≅ △ ADE
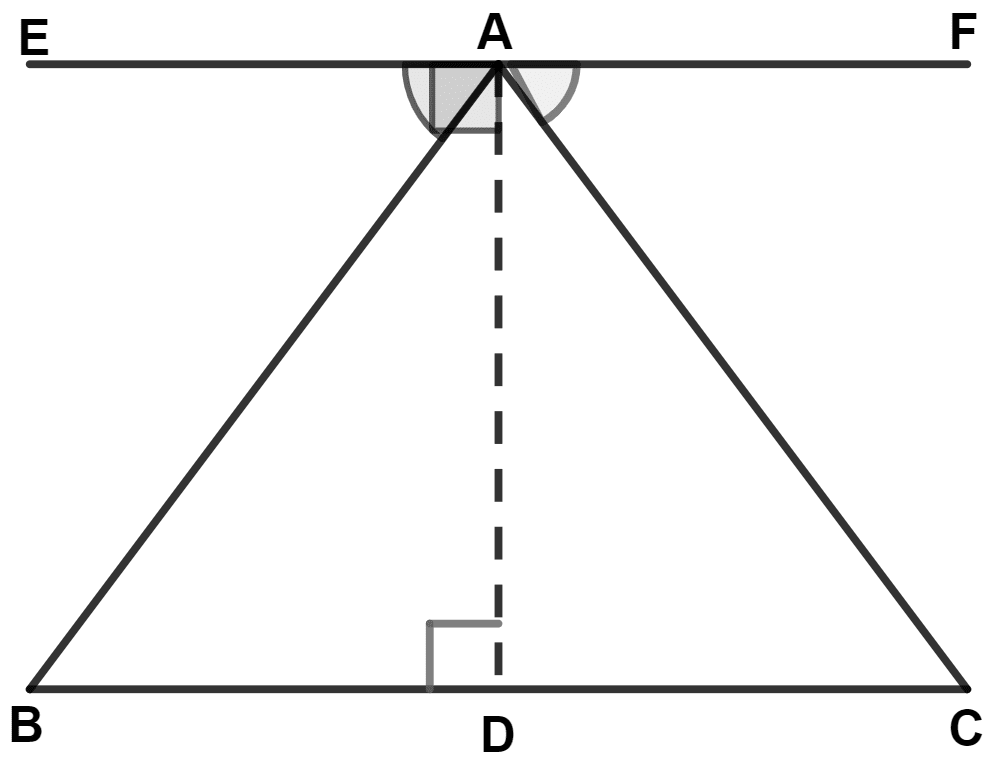
Which of the following is true for the given figure :
△ ABD ≅ △ ACD
angle BAD ≠ angle CAD
△ ABD ≇ △ ACD
∠EAB = ∠BAD
In the given figure, BC // DA and BC = DA, then :
AB and CD bisect each other
AB ≠ CD
OA = OC
OA = OD
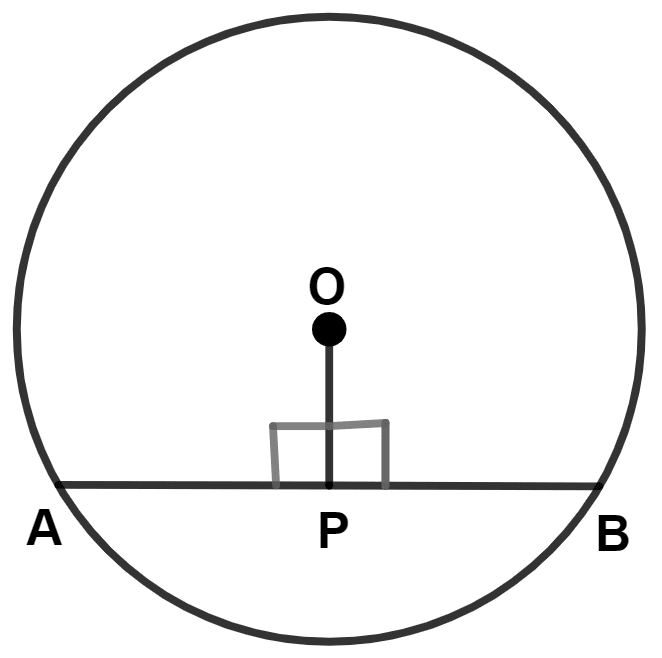
The following figure shows a circle with center O. If OP is perpendicular to AB, prove that AP = BP.