Mathematics
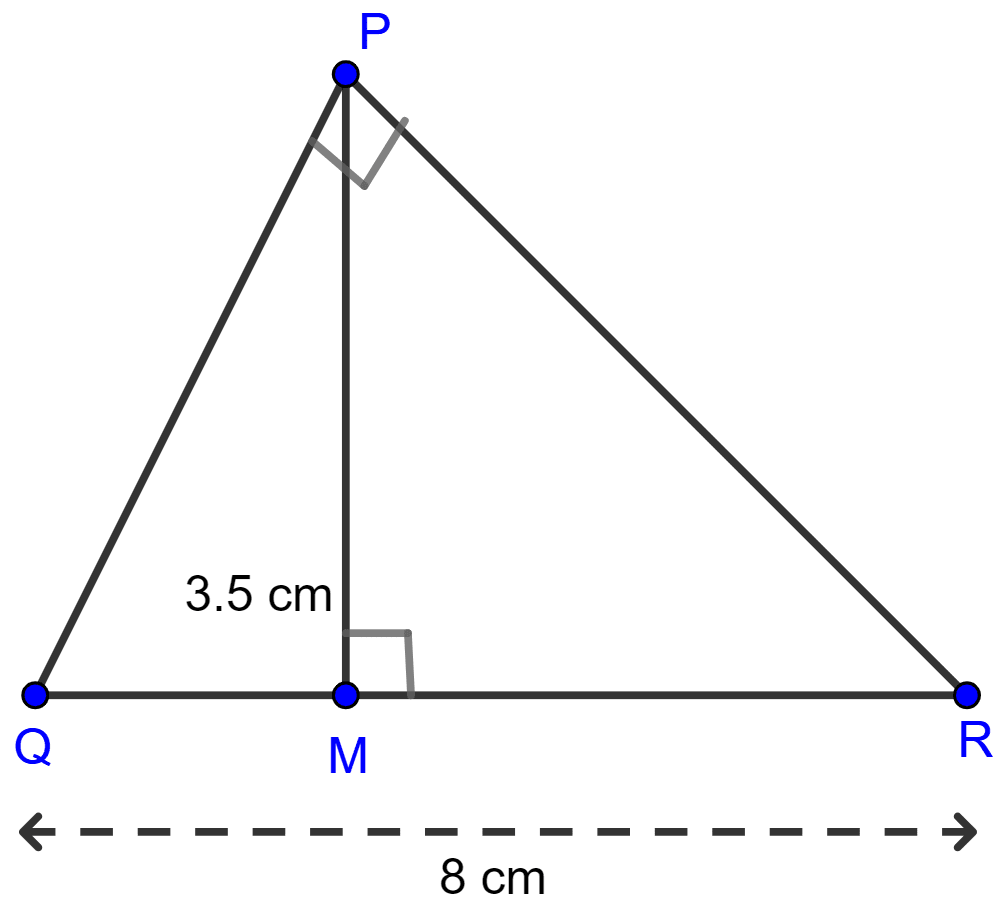
In the right-angled triangle QPR. PM is an altitude.
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
Similarity
20 Likes
Answer
In △PQR and △MPR,
∠QPR = ∠PMR = 90°
∠PRQ = ∠PRM (Common)
∴ △PQR ~ △MPR [By AA]
Since, corresponding sides of similar triangle are proportional to each other.
Hence, PR = 6 cm.
Answered By
15 Likes
Related Questions
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that :
(i) △EGD ~ △CGB and
(ii) BG = 2GD from (i) above.
In the given figure, AB || EF || DC; AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm.
(i) Name the three pairs of similar triangles.
(ii) Find the length of EC and EF.
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC.
Show that angle BAC = 90°.
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
(i) Calculate the ratio PQ : AC, giving reason for your answer.
(ii) In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.
