Mathematics
In triangle ABC, AB > AC and D is a point in side BC. Show that :
AB > AD.
Triangles
8 Likes
Answer
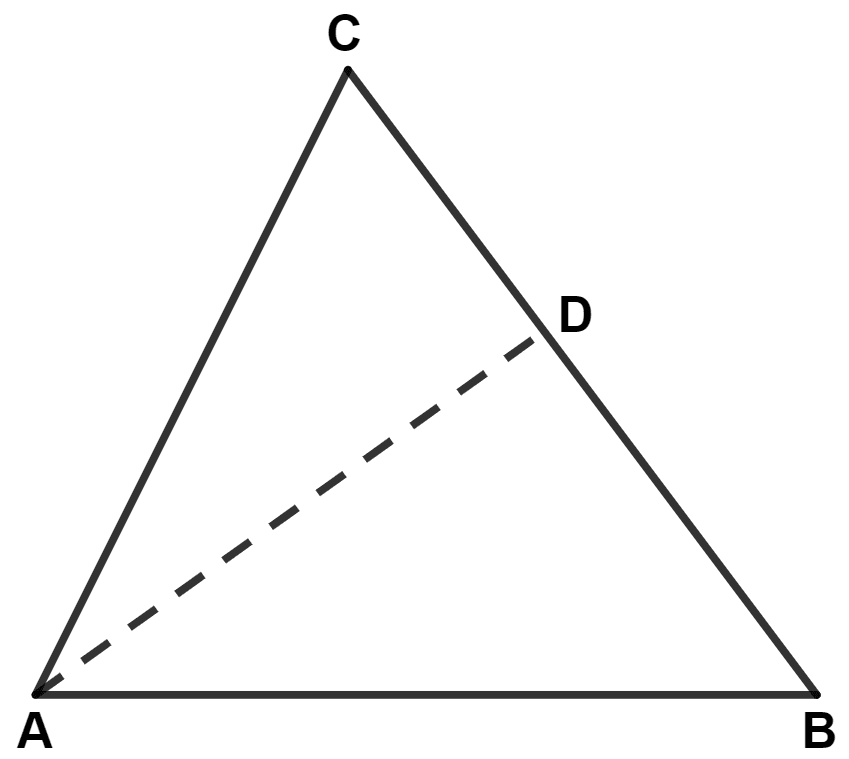
In △ ABC,
⇒ AB > AC (Given)
⇒ ∠C > ∠B (If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.)
In △ ADC,
⇒ ∠ADB = ∠DAC + ∠C (In a triangle an exterior angle is equal to sum of two opposite interior angles)
We can say that,
⇒ ∠ADB > ∠C
Since, ∠ADB > ∠C and ∠C > ∠B,
∴ ∠ADB > ∠B
In △ ADB,
Since, ∠ADB > ∠B
∴ AB > AD (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)
Hence, proved that AB > AD.
Answered By
4 Likes
Related Questions
In quadrilateral ABCD, side AB is the longest and side DC is the shortest. Prove that :
(i) ∠C > ∠A
(ii) ∠D > ∠B
In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : ∠ADC is greater than ∠ADB.
In isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i) AC > AD
(ii) AE > AC
(iii) AE > AD
Given : ED = EC
Prove : AB + AD > BC.