Mathematics
In triangle ABC; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
Mid-point Theorem
7 Likes
Answer
By mid-point theorem,
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.
By converse of mid-point theorem,
The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.
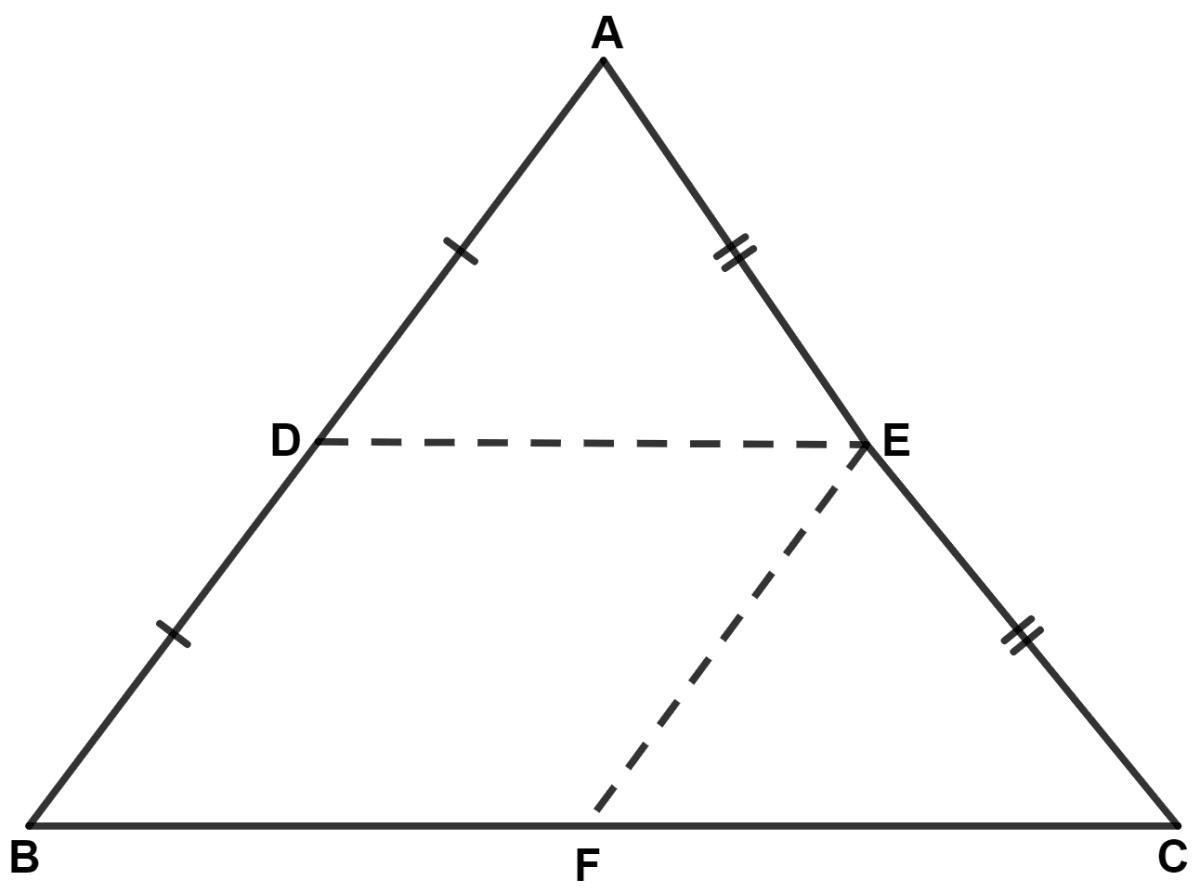
Given,
E is mid-point of AC and EF || AB.
∴ F is mid-point of BC (By converse of mid-point theorem).
Since, D and E are mid-points of sides AB and AC respectively.
∴ DE || BC and DE = (By mid-point theorem)
⇒ DE || BF and DE = BF (As F is mid-point of BC).
Given,
EF || BC
∴ EF || BD.
Since, E and F are mid-points of sides AC and BC respectively.
∴ EF = = BD. (By mid-point theorem)
Since, opposite sides of quadrilateral BDEF are parallel and equal.
∴ BDEF is a parallelogram.
From figure,
⇒ BD = = 8 cm,
⇒ BF = = 9 cm.
Perimeter of BDEF = BD + DE + EF + BF
= BD + BF + BD + BF (Since opposite sides of parallelogram are equal)
= 8 + 9 + 8 + 9
= 34 cm.
Hence, perimeter of parallelogram BDEF = 34 cm.
Answered By
3 Likes
Related Questions
In △ ABC, E is mid-point of the median AD and BE produced meets side AC at point Q. Show that BE : EQ = 3 : 1.
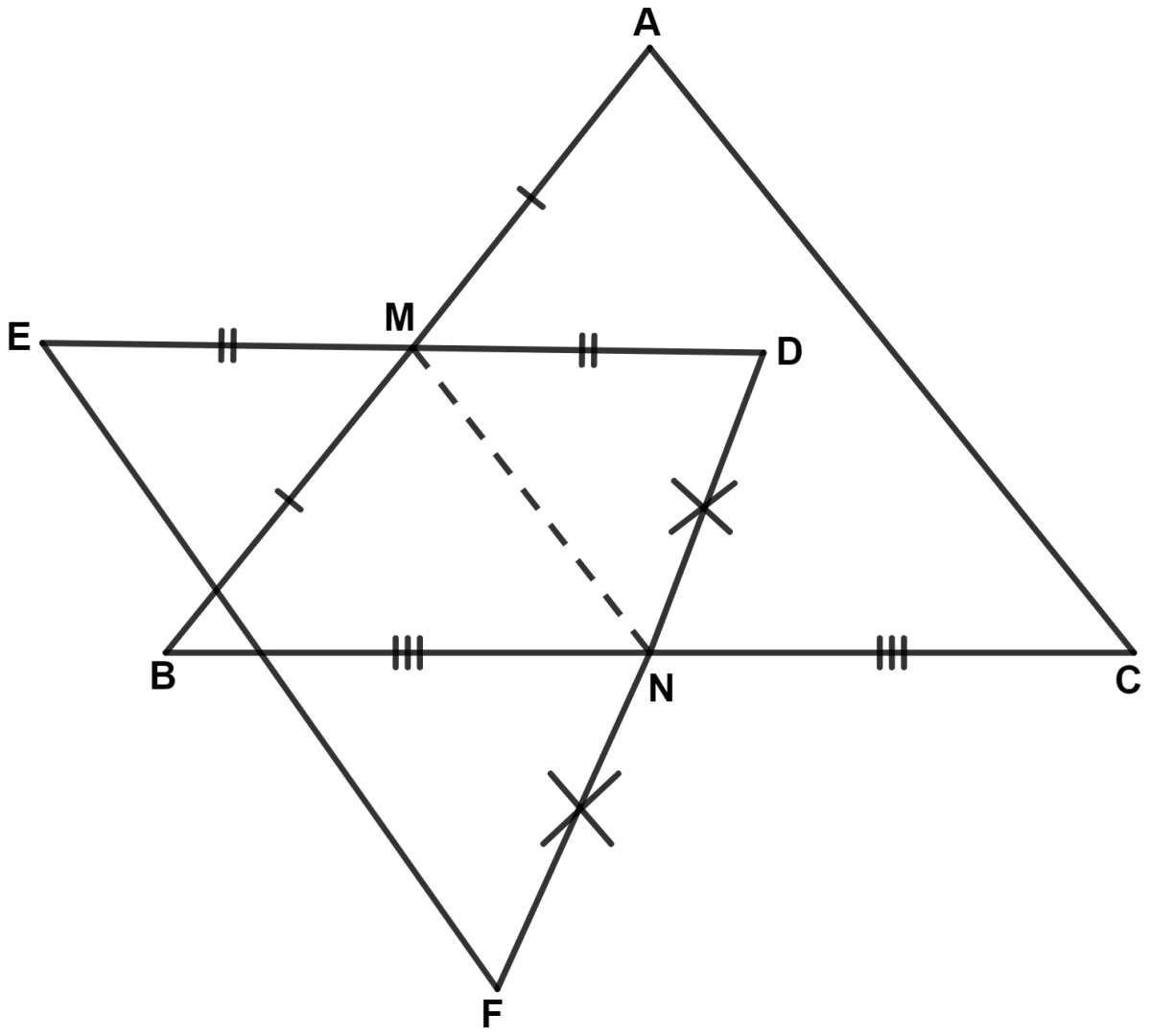
In the given figure, M is the mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
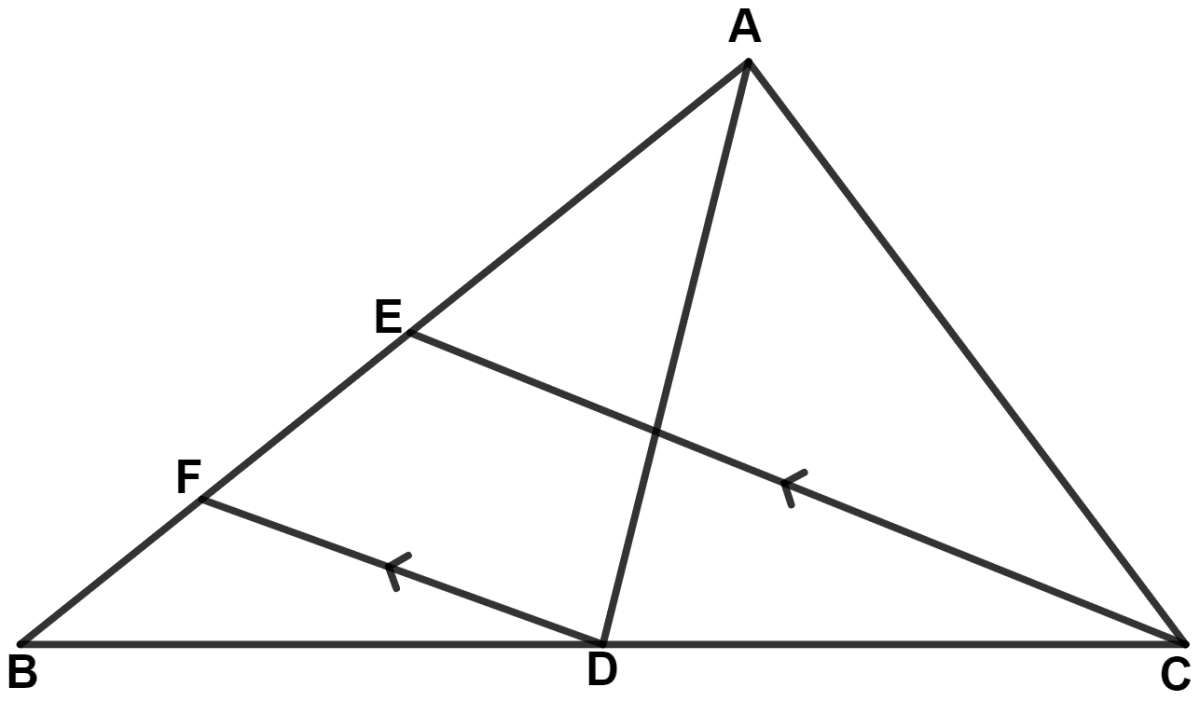
In the given figure, AD and CE are medians and DF // CE. Prove that : FB = .
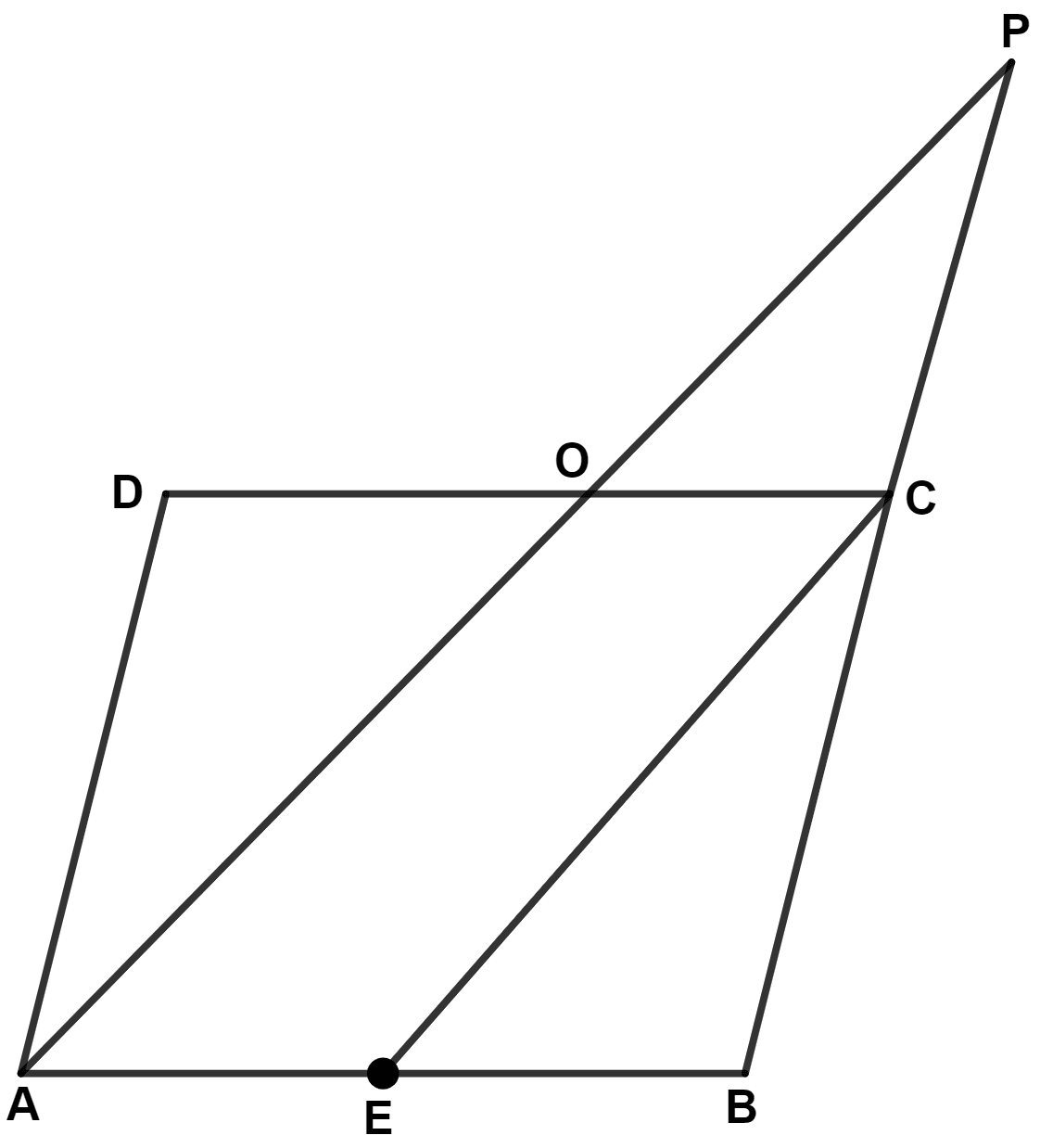
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
(i) BP = 2AD
(ii) O is mid-point of AP.