Mathematics
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.
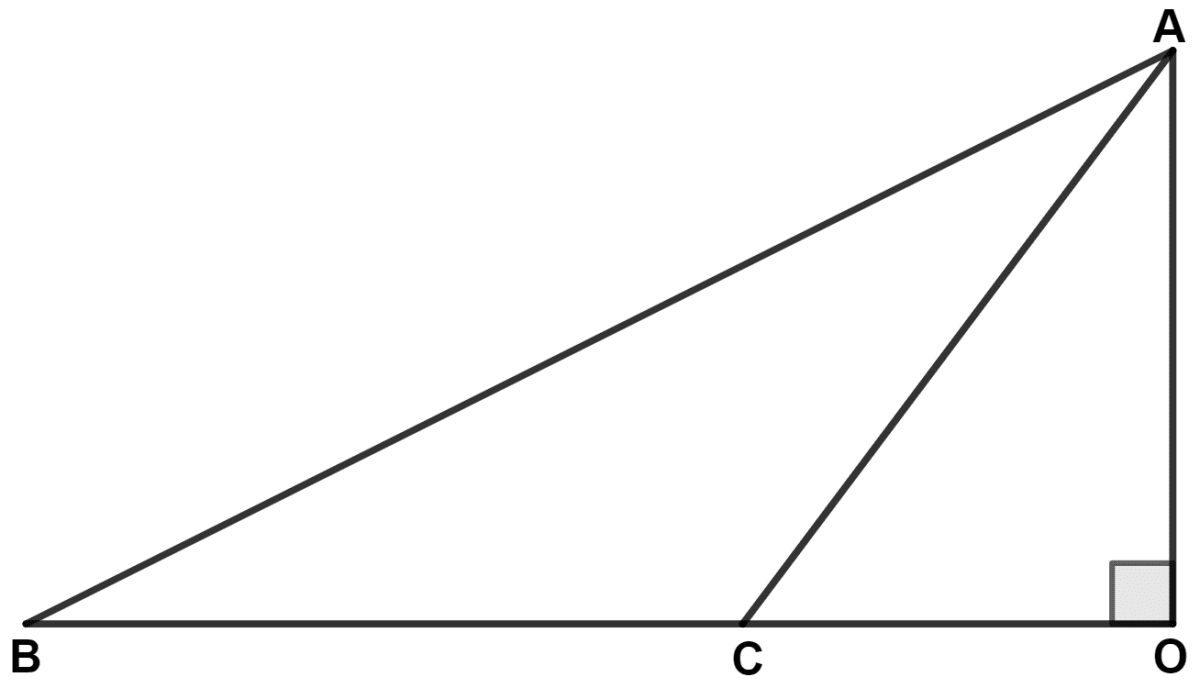
Pythagoras Theorem
77 Likes
Answer
Let length of OC be x cm.
In right angled triangle AOC,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ AC2 = AO2 + OC2
⇒ 32 = AO2 + x2
⇒ AO2 = 32 - x2
⇒ AO2 = 9 - x2
⇒ AO = cm.
From figure,
BO = BC + CO = (6 + x) cm.
In right angled triangle AOB,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ AB2 = AO2 + BO2
⇒ 82 = + (6 + x)2
⇒ 64 = 9 - x2 + 36 + x2 + 12x
⇒ 64 = 45 + 12x
⇒ 12x = 64 - 45
⇒ 12x = 19
⇒ x = .
Hence, OC = cm.
Answered By
46 Likes
Related Questions
In a quadrilateral PQRS, ∠Q = ∠S = 90° then prove that 2PR2 - QR2 = PQ2 + PS2 + SR2.
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
In triangle ABC,
AB = AC = x; BC = 10 cm and the area of the triangle is 60 cm2. Find x.
If the sides of a triangle are in the ratio 1 : : 1, show that it is a right-angled triangle.