Mathematics
The length of the ladder placed against a vertical wall is twice the distance between the foot of the ladder and the wall.
Assertion(A): The angle that the ladder makes with the wall is 60°.
Reason(R): If ladder makes angle θ with the wall then sin θ = .
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Heights & Distances
3 Likes
Answer
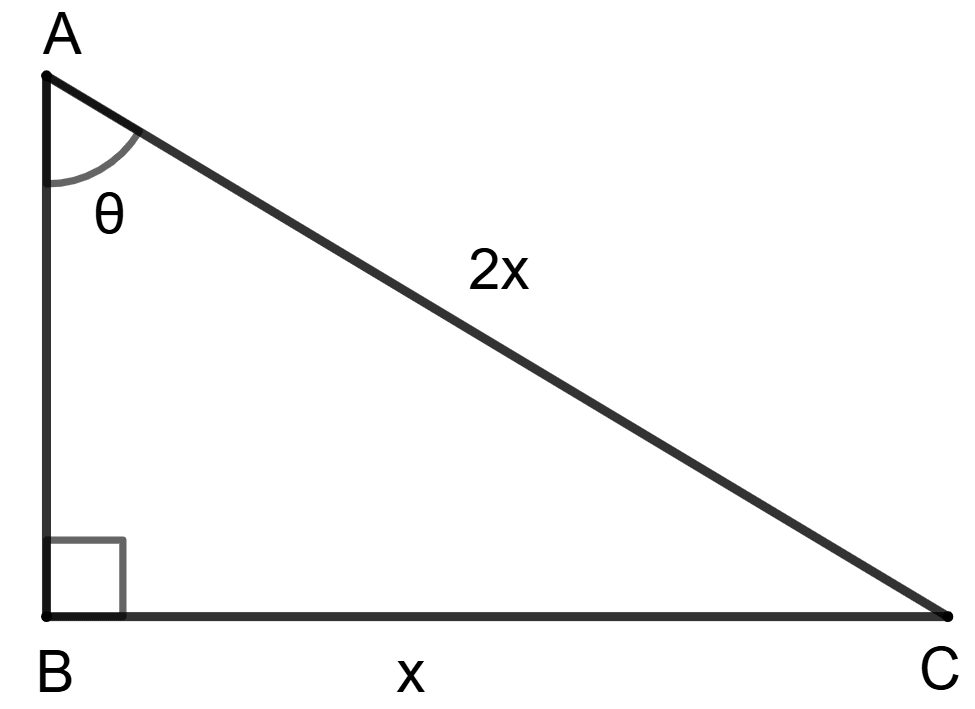
Let AB be the wall and AC be the ladder. Let distance between foot of ladder and wall be x.
So, length of ladder (AC) = 2x.
According to the Pythagoras theorem :
⇒ Hypotenuse2 = Base2 + Height2
⇒ AC2 = BC2 + AB2
⇒ (2x)2 = x2 + AB2
⇒ 4x2 = x2 + AB2
⇒ AB2 = 4x2 - x2
⇒ AB2 = 3x2
⇒ AB =
⇒ AB = .
Let angle between ladder and wall be θ.
We know that,
⇒ sin θ = sin 30°
⇒ θ = 30°.
Assertion (A) is false.
If ladder makes angle θ with the wall then sin θ = .
Here base refers side opposite to angle θ i.e. BC.
Reason (R) is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
The length of DC is :
m
m
m
m

The ratio of the length of a vertical pole and length of its shadow on the horizontal surface is 3 :
Assertion(A): The angle of elevation of the sun is 60°.
Reason(R): If angle of elevation of the sun is θ, tan θ = = tan 60°.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
For the following figure, tan A = and tan B =
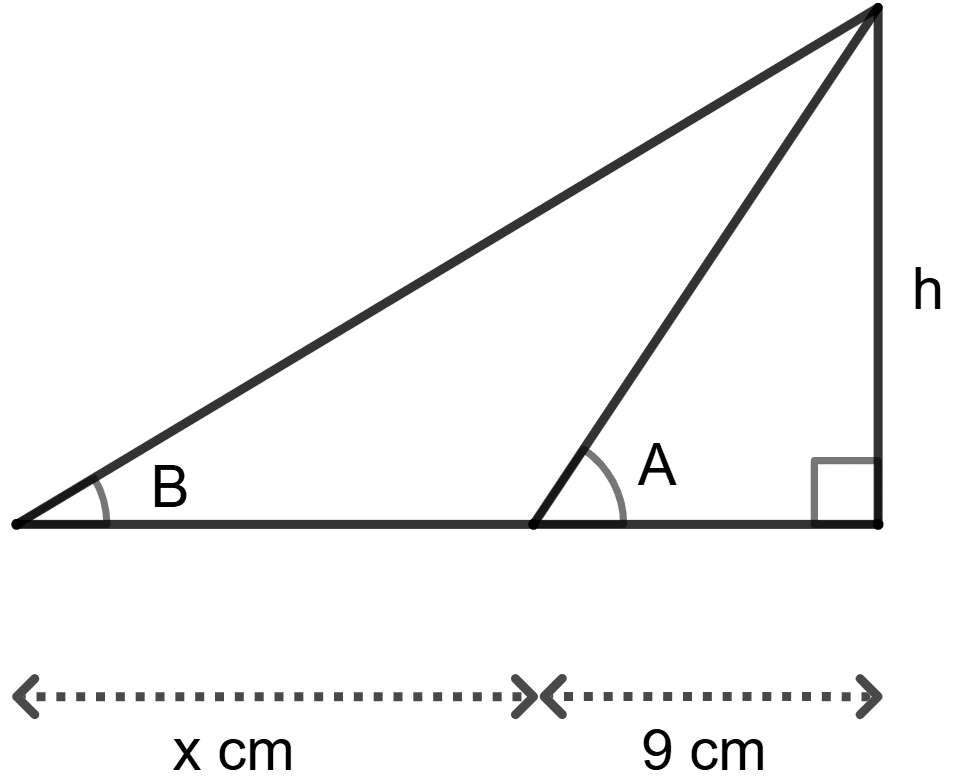
Statement (1): x = 36 cm
Statement (2): tan A = ⇒ h = 15
tan B =
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
CD = 100 m, ∠ADB = 15° and ∠BDC = 45°
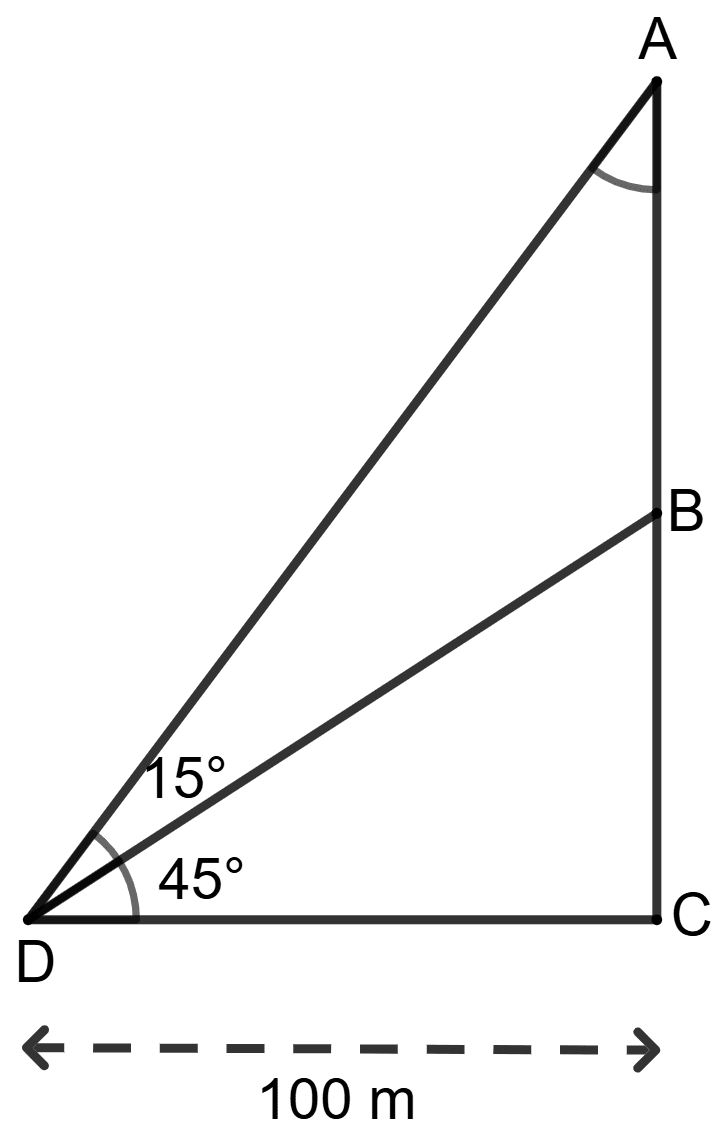
Statement (1): AB =
Statement (2): AB = (100 tan 60° - 100 tan 45°) m.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.