KnowledgeBoat Logo
|

Mathematics

Let A = {x ∈ R : 11x - 5 > 7x + 3} and B = {x ∈ R : 8x - 9 ≥ 15 + 2x}. Find A ∩ B and represent it on the number line.

Linear Inequations

2 Likes

Answer

Given,

A = {x ∈ R : 11x - 5 > 7x + 3}

⇒ 11x - 5 > 7x + 3

⇒ 11x - 7x > 3 + 5

⇒ 4x > 8

⇒ x > 84\dfrac{8}{4}

⇒ x > 2

Since, x ∈ R,

A = {x : x > 2, x ∈ R}

Given,

B = {x ∈ R : 8x - 9 ≥ 15 + 2x}

⇒ 8x - 9 ≥ 15 + 2x

⇒ 8x - 2x ≥ 15 + 9

⇒ 6x ≥ 24

⇒ x ≥ 246\dfrac{24}{6}

⇒ x ≥ 4

Since, x ∈ R

B = {x : x ≥ 4, x ∈ R}

A ∩ B = Numbers common between A and B = {x : x ≥ 4, x ∈ R}

Hence, A ∩ B = {x : x ≥ 4, x ∈ R}.

Solution on the number line is :

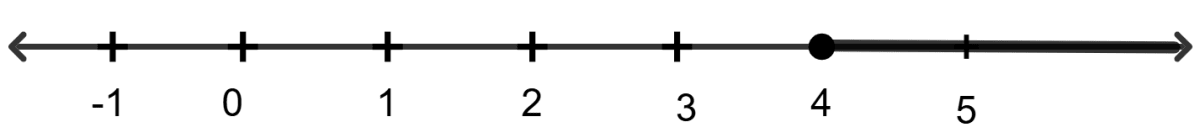
Let A = {x ∈ R : 11x - 5 > 7x + 3} and B = {x ∈ R : 8x - 9 ≥ 15 + 2x}. Find A ∩ B and represent it on the number line. Linear Inequations, RSA Mathematics Solutions ICSE Class 10.

Answered By

3 Likes

Related Questions