Mathematics
A line segment joining P (2, -3) and Q (0, -1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S. Find the :
(a) equation of line PQ
(b) equation of line AB
(c) coordinates of points R and S.
Straight Line Eq
ICSE Sp 2025
257 Likes
Answer
(a) By formula,
Slope of line =
Substituting values we get :
Equation of line :
⇒ y - y1 = m(x - x1)
⇒ y - (-3) = -1(x - 2)
⇒ y + 3 = -x + 2
⇒ x + y + 3 - 2 = 0
⇒ x + y + 1 = 0.
Hence, equation of line PQ is x + y + 1 = 0.
(b) We know that,
Product of slope of perpendicular lines = -1.
∴ Slope of PQ × Slope of AB = -1
⇒ -1 × Slope of AB = -1
⇒ Slope of AB = = 1.
Equation of line :
⇒ y - y1 = m(x - x1)
Equation of line AB :
⇒ y - 6 = 1(x - 0)
⇒ y - 6 = x
⇒ x - y + 6 = 0
Hence, equation of line AB is x - y + 6 = 0.
(c) Given,
Line PQ cuts x-axis at point R.
Let R = (a, 0)
Equation of line PQ = x + y + 1 = 0
Since, point R lies on line PQ,
⇒ a + 0 + 1 = 0
⇒ a + 1 = 0
⇒ a = -1.
R = (a, 0) = (-1, 0)
Given,
AB is perpendicular to PQ at point S.
∴ Point S is the intersection point of AB and PQ.
PQ : x + y + 1 = 0
AB : y - x = 6 or y = x + 6
Substituting value of y from equation AB in equation PQ, we get :
⇒ x + (x + 6) + 1 = 0
⇒ 2x + 7 = 0
⇒ 2x = -7
⇒ x =
Substituting value of x in equation AB, we get :
y = .
S = .
Hence, coordinates of R = (-1, 0) and S = .
Answered By
168 Likes
Related Questions
Given, x + 2 ≤ and x is a prime number. The solution set for x is :
∅
{0}
{1}
{0, 1}
While factorizing a given polynomial, using remainder and factor theorem, a student finds that (2x + 1) is a factor of 2x3 + 7x2 + 2x - 3.
(a) Is the student's solution correct stating that (2x + 1) is a factor of the given polynomial ? Given a valid reason for your answer.
(b) Factorize the given polynomial completely.
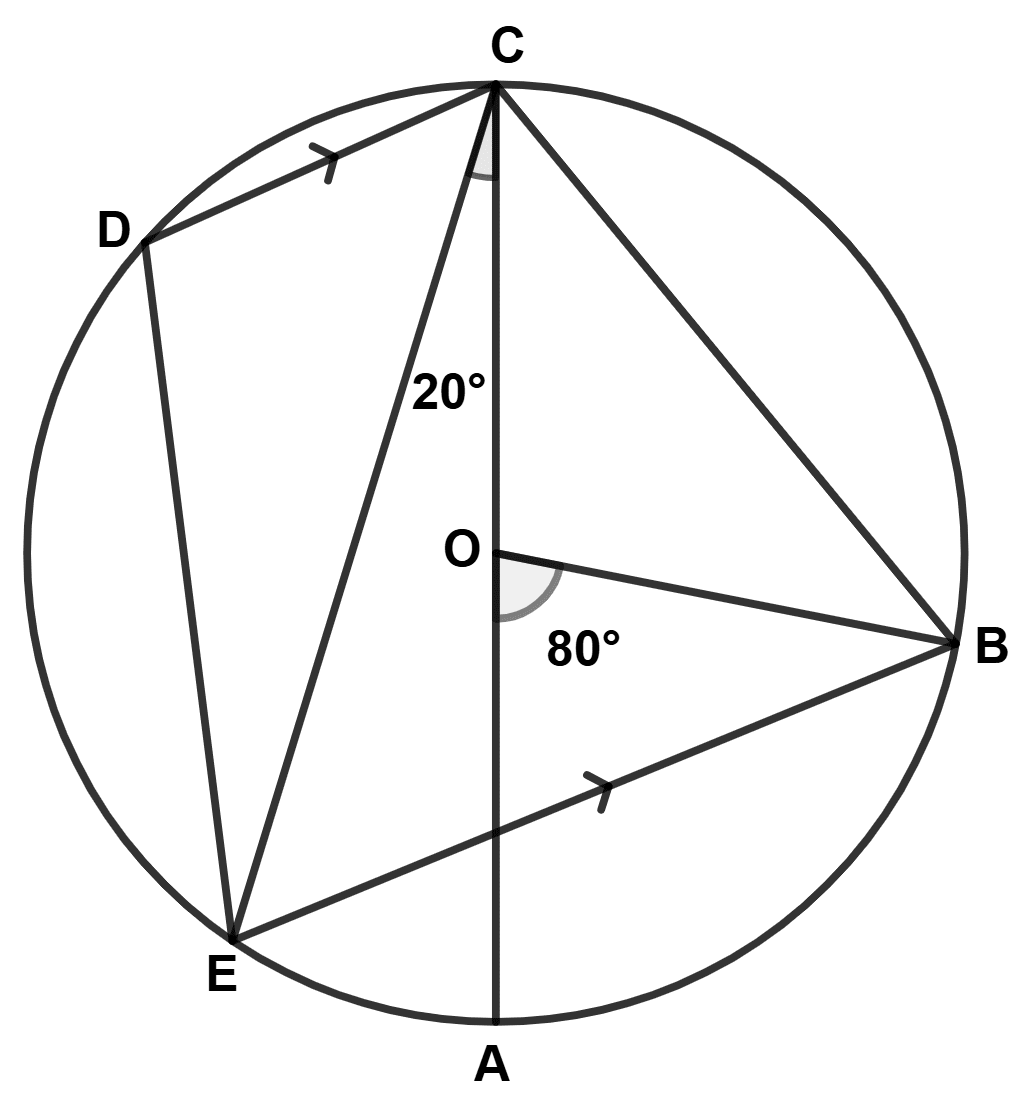
In the given figure AC is the diameter of the circle with center O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°. Calculate :
(a) ∠BEC
(b) ∠BCD
(c) ∠CED
In a Geometric Progression (G.P.) the first term is 24 and the fifth term is 8. Find the ninth term of the G.P.