Mathematics
M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O. Prove that :
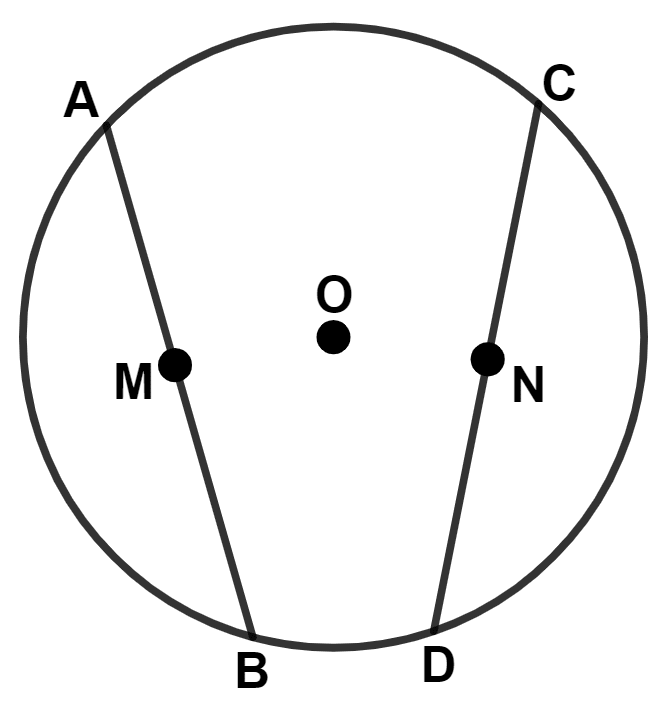
(i) ∠BMN = ∠DNM
(ii) ∠AMN = ∠CNM.
Circles
59 Likes
Answer
Join OM, ON, OB and OD.
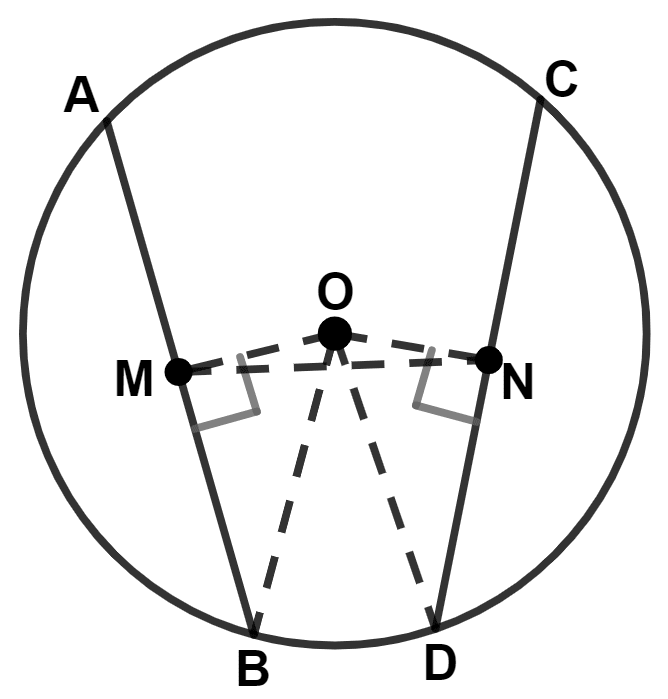
Given,
M and N are the mid-points of two equal chords AB and CD.
∴ BM = and DN =
Since, AB and CD are equal chords.
∴ BM = DN ……….(1)
We know that,
A straight line drawn from the center of a circle to bisect a chord, which is not a diameter, is at right angles to the chord.
∴ OM ⊥ AB and ON ⊥ CD.
∴ ∠OMB = ∠OND (Both equal to 90°) ……..(2)
(i) In triangle OMN,
⇒ ON = OM (Equal chords of a circle are equidistant from the center.)
⇒ ∠OMN = ∠ONM (Angles opposite to equal sides are equal) ……..(3)
Subtracting equation (2) from (3), we get :
⇒ ∠OMB - ∠OMN = ∠OND - ∠ONM
⇒ ∠BMN = ∠DNM.
Hence, proved that ∠BMN = ∠DNM.
(ii) From figure,
⇒ ∠OMA = ∠ONC (Both equal to 90°) ……………(4)
Adding equation (3) and (4), we get :
⇒ ∠OMA + ∠OMN = ∠ONC + ∠ONM
⇒ ∠AMN = ∠CNM.
Hence, proved that ∠AMN = ∠CNM.
Answered By
46 Likes
Related Questions
A chord CD of a circle, whose center is O, is bisected at P by a diameter AB.
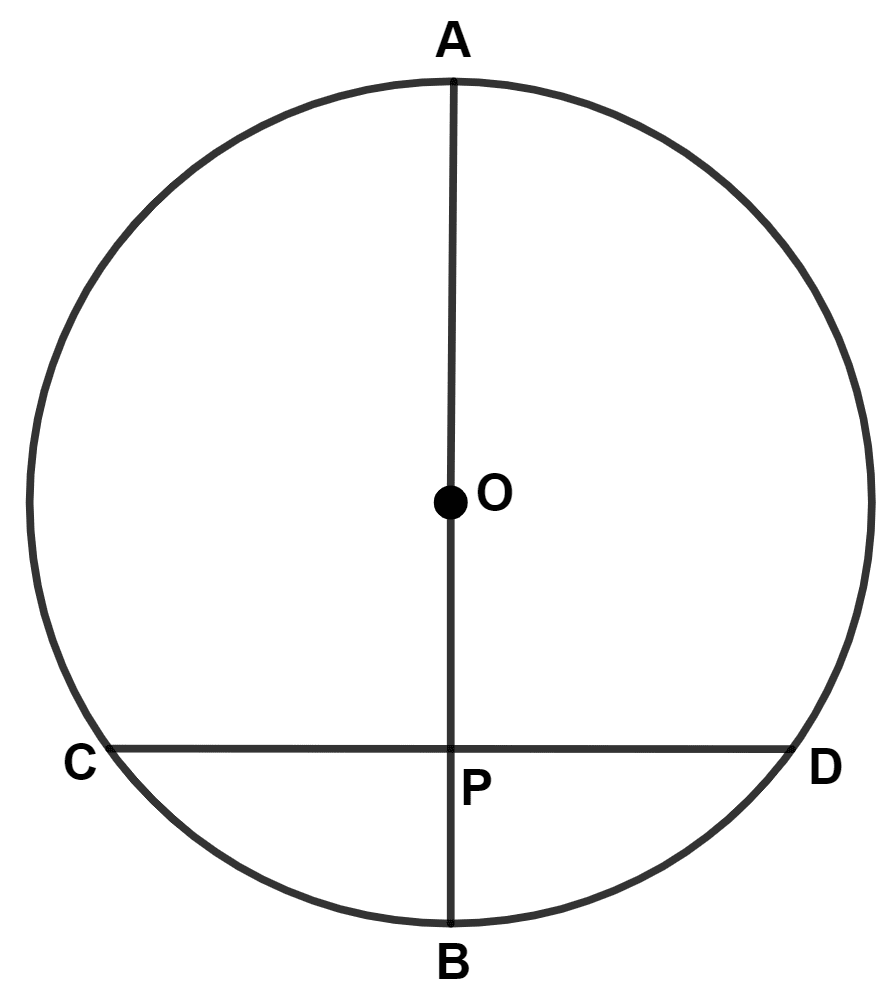
Given OA = OB = 15 cm and OP = 9 cm. Calculate the lengths of :
(i) CD
(ii) AD
(iii) CB.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'.
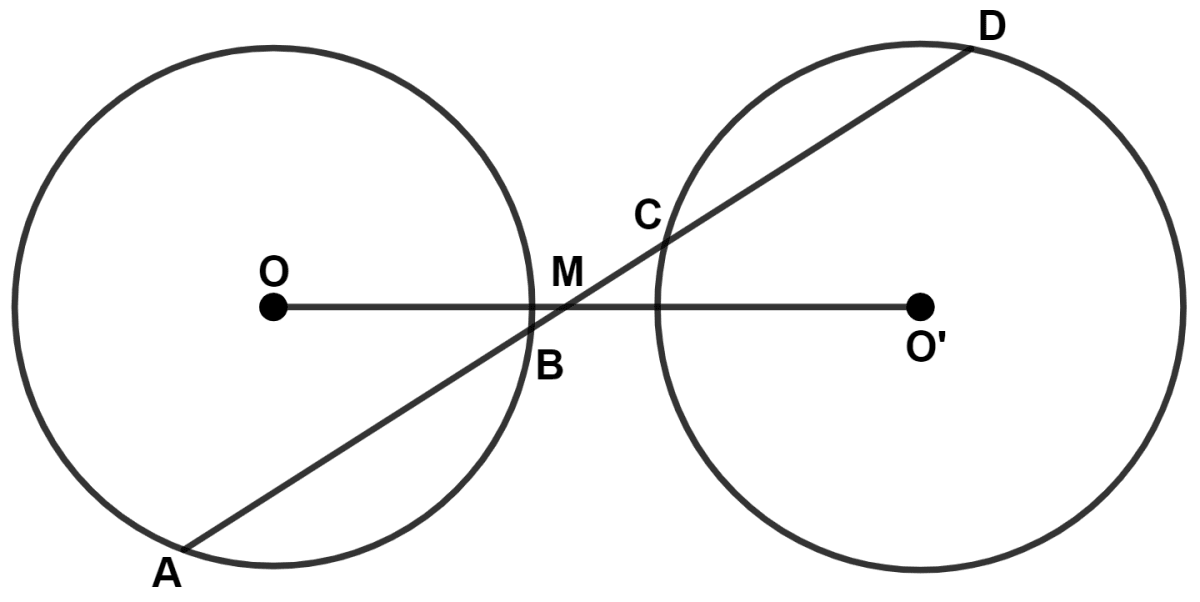
Prove that the chords AB and CD, which are intercepted by the two circles, are equal.
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle. Prove that :
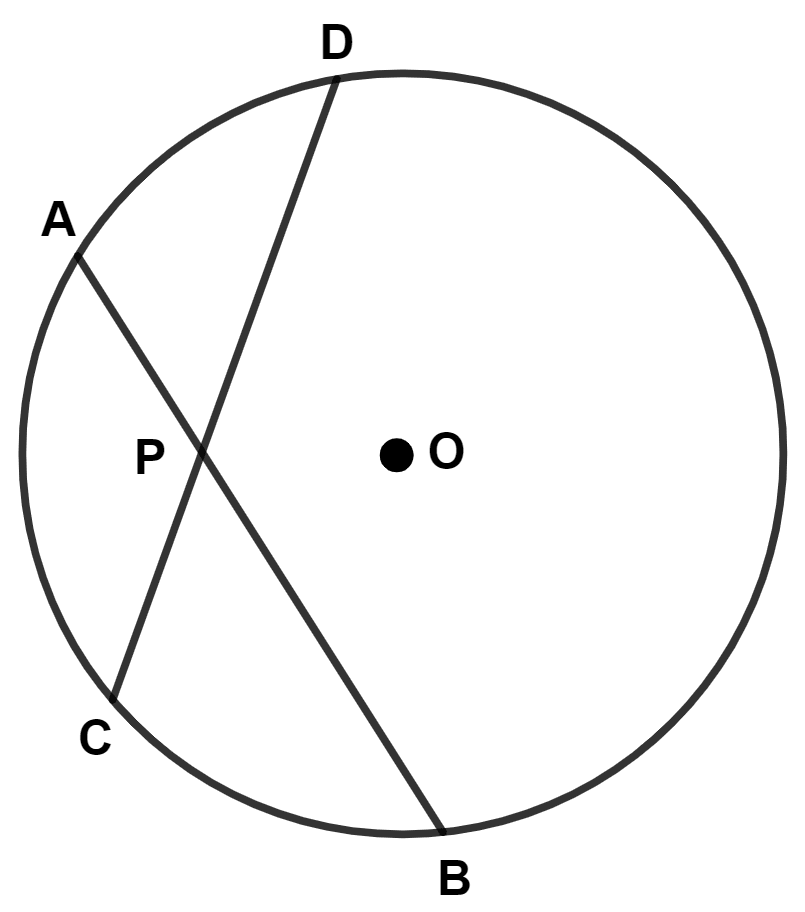
(i) AP = CP
(ii) BP = DP
In the following figure, OABC is a square. A circle is drawn with O as center which meets OC at P and OA at Q. Prove that :
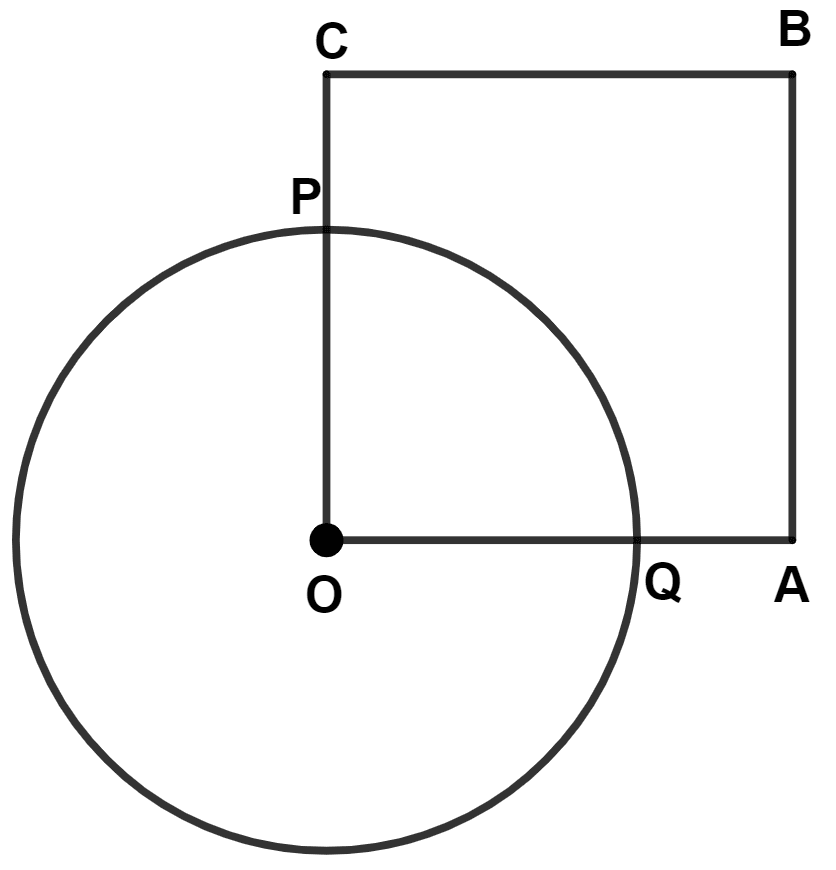
(i) △ OPA ≅ △ OQC
(ii) △ BPC ≅ △ BQA