Mathematics
M is a fixed point in a plane and a point P moves in the same plane such that PM = 10 cm. State :
(i) the name of the figure formed.
(ii) the length of the radius of the circle.
(iii) the length of the diameter of the circle.
Can a chord of length 16 cm can be drawn in this circle? Give reason.
Circles
3 Likes
Answer
(i) Given, M is a fixed point. P moves such that PM = 10 cm.
A circle is a set of points equidistant from a center or a fixed point.
Hence, the figure is circle with M as center.
(ii) M is the center of the circle and PM is the radius of the circle.
Hence, the length of the radius of the circle = 10 cm.
(iii) As we know that the diameter is twice the radius.
Diameter = 2 x 10 cm = 20 cm
Hence, the length of the diameter of the circle = 20 cm.
The longest chord is the diameter.
The diameter is 20 cm.
A chord of length 16 cm can be drawn since 16 < 20.
Hence, a chord of length 16 cm can be drawn in this circle.
Answered By
2 Likes
Related Questions
Assertion (A) : A, B and C are three points on the circumference of a circle such that BC is diameter of the circle. If AC = 4 cm and AB = 3 cm, then diameter BC = 4 cm + 3 cm.
Reason (R) : Angle BAC = angle of semi-circle = 90° and so BC2 = AB2 + AC2
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
The following figure shows the circle with centre O.
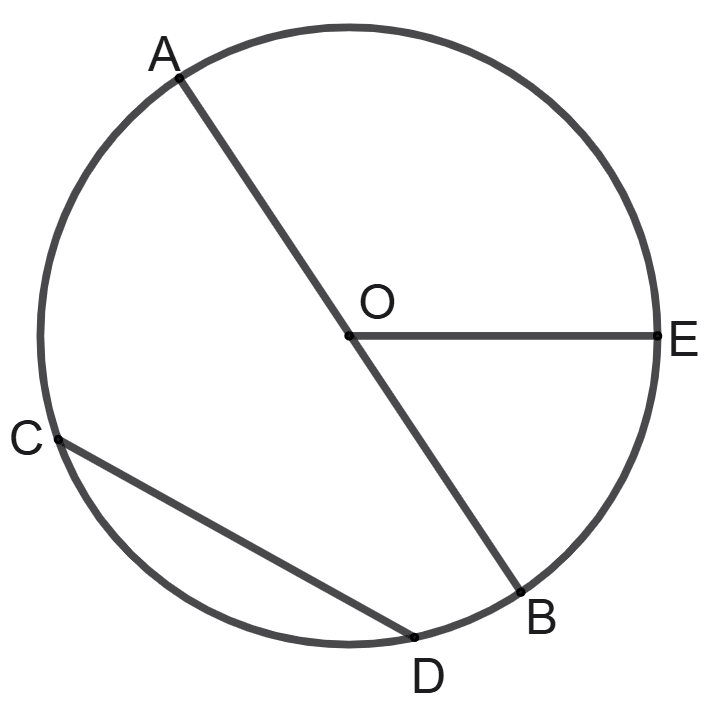
Use the figure to fill the blanks in each of the following :
(i) AB = ……………..
(ii) Radius = …………….
(iii) Chords = ……….. and ………..
(iv) Diameter = …………
(v) AB = 2 x ………….
The radius of a circle is 6 cm. Find its diameter. If O is the centre of the circle; state, giving reasons, the position of points A, B and C; if;
(i) OA = 4.8 cm
(ii) OB = 7.5 cm
(iii) OC = 6 cm
Fill in the blanks :
(i) An arc is the part of the ……………….
(ii) Diameter of a circle bisects …………
(iii) The part of the circumference greater than the semicircle is called …………….
(iv) Sector of a circle is its region bounded by ……………..
(v) The segment of a circle is the region bounded by ………………
(vi) A tangent of a circle meets the circle at …………..
(vii) The number of tangents that can be drawn through a point on its circumference = ……………
(viii) The number of tangent that can be drawn through a point outside the circle is ……………..