Physics
(a) A man fires a gun and hears its echo after 3 s. The man then moves 80 m towards the hill and fires his gun again. This time he hears the echo after 2.5 s. Calculate the speed of the sound.
(b) State one reason of using ultrasonic waves in SONAR.
Sound
3 Likes
Answer
Given,
- Time to hear first echo (t1) = 3 s
- Time to hear second echo (t2) = 2.5 s
- Distance moved by the man towards the hill (d) = 80 m
(a) Let original distance of the man from the cliff is 'D' and speed of sound be 'v'.
Case 1 : When person hears first echo from initial position.
Case 2 : When person hears second echo after moving 80 m towards the cliff.
New distance between the man and the cliff = D - d = - 80
Then,
⇒ v = 80 x 4 = 320 m s-1
Hence, speed of the sound is 320 m s-1.
(b) Ultrasonic waves can travel undeviated through a long distance and that's why they are used in SONAR.
Answered By
1 Like
Related Questions
An inclined plane makes an angle of 30° with the horizontal as shown in the figure. A box of mass 20 kg is taken from point A to point B along the inclined plane of length 2 m.
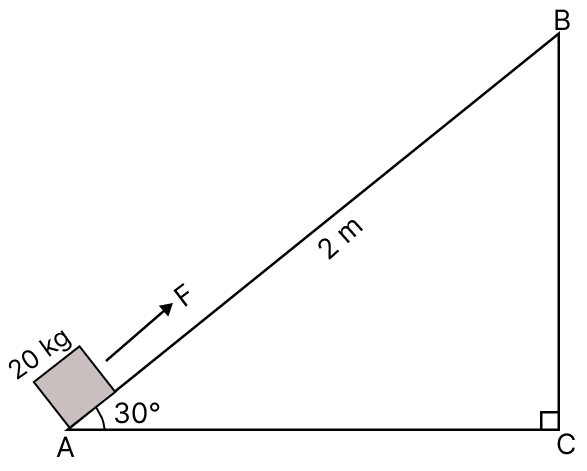
(a) Calculate the potential energy gained by the box.
(b) If 10 J of work is done against friction, in moving the box from A to B then calculate the force F needed to pull the block from A to B. [g = 10 m s-2]
The graph shows load against effort for a lever with load and effort on the same side of the fulcrum.
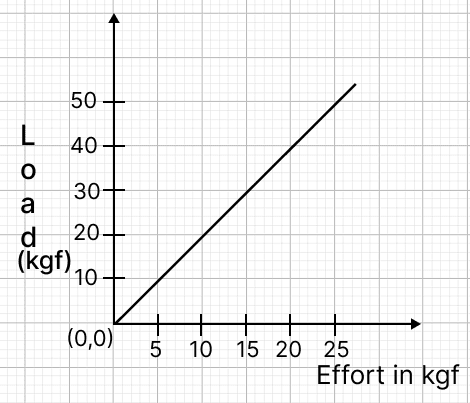
(a) Which attribute of the load vs effort graph must be calculated to determine the mechanical advantage?
(b) Which class does this lever belong to? How did you arrive at this conclusion?
The diagram below displays four solid plastic balls attached to wires, all mounted on a wooden base. When a person shakes the wooden base back and forth at a steady pace, the balls begin to vibrate as well. It is noted that while all the balls vibrate, only one of them vibrates vigorously.
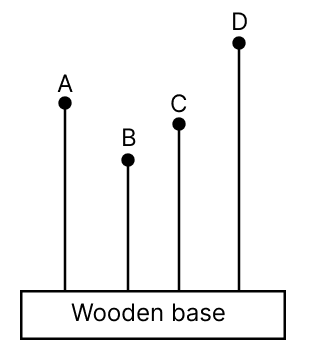
(a) Explain why only one ball vibrates vigorously.
(b) If fA, fB, fC, and fD are the natural frequencies of vibration of the wires, then arrange them in the increasing order of their frequencies and justify.
The diagram given below shows a bulb connected by dual control switches. Observe the diagrams and answer the questions that follow.
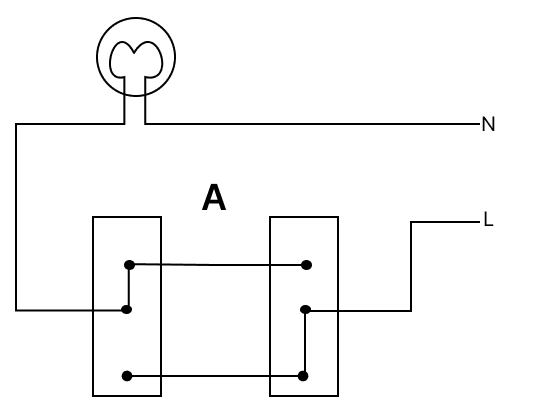
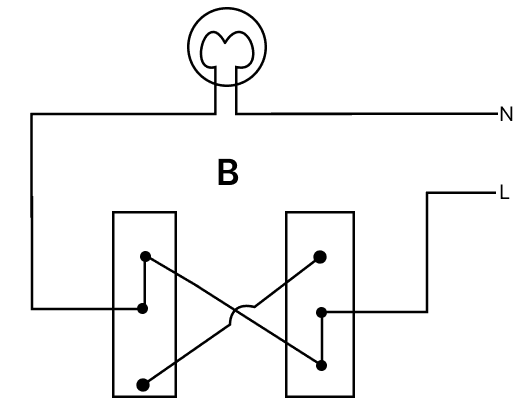
(a) Which switch can successfully turn the bulbs ON or OFF? (Circuit A, Circuit B, or both)
(b) At present, in which circuit is the bulb glowing?
(c) If the L and N wires are swapped in the circuit (your answer to (b)), will the circuit still function?