Physics
A metal rod AB of length 80 cm is balanced at 45 cm from the end A with 100 gf weights suspended from the two ends.
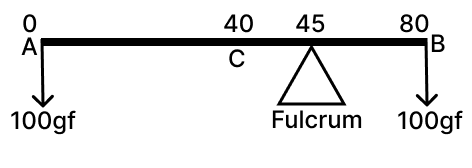
(a) If this rod is cut at the centre C, then compare the weight of AC to the weight of BC.
(b) Give a reason for your answer in (a)
Force
14 Likes
Answer
Given,
Weight at the end A (WA) = 100 gf
Weight at the end B (WB) = 100 gf
Length of the rod (L) = 80 cm
Distance of A from the fulcrum (lA) = 45 cm
Distance of B from the fulcrum (lB) = 80 cm - 45 cm = 35 cm
Let,
Weight of the rod AC is (WAC) and distance of centre of gravity of the rod AC from the fulcrum is (lAC).
And
Weight of the rod BC is (WBC) and distance of centre of gravity of the rod BC from the fulcrum is (lBC).
Here,
(lAC) = 45 - 20 = 25 cm,
(lBC) = 60 - 45 = 15 cm,
Now,
Anticlockwise moment (due to weight of 100 gf at end A and weight of rod AC) = lA x WA + lAC x WAC = 45 x 100 + 25 x WAC
Clockwise moment (due to weight of 100 gf at end B and weight of rod BC) = lB x WB + lBC x WBC = 35 x 100 + 15 x WBC
As system is balanced then for equilibrium,
Anticlockwise moment of force about the fulcrum = Clockwise moment of force about the fulcrum
45 x 100 + 25 x WAC = 35 x 100 + 15 x WBC
⇒ 4500 + 25WAC = 3500 + 15WBC
⇒ 15WBC - 25WAC = 4500 - 3500 = 1000
⇒ 3WBC - 5WAC = 200
⇒ 3WBC - 5WAC > 0
⇒ 3WBC > 5WAC
⇒ WBC > WAC
Hence, weight of AC < weight of BC.
(b) Even though the weights present are the same at both ends and the torque arm of B is less than the torque arm of A. This means the moment of the weight of the rod acts from side B and the C.G. lies beyond 45. Thus, more weight is concentrated between C to B.
Answered By
8 Likes
Related Questions
When sunlight passes through water droplets in the atmosphere it gets dispersed into its constituent colours forming a rainbow. A similar phenomenon is observed when white light passes through a prism.
(a) Which colour will show the maximum angle of deviation and which colour will show the minimum angle of deviation?
(b) If Instead of sunlight, a green-coloured ray is passed through a glass prism. What will be the colour of the emergent ray?
O is a luminescent particle trapped inside a glass block. A student traces the path of rays coming out of it and reflecting over a plane mirror as shown in the diagram below.
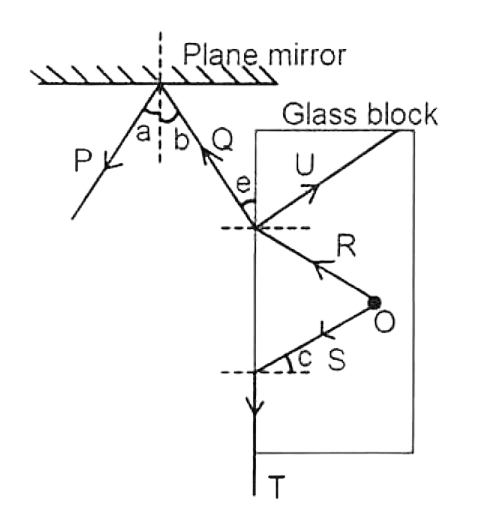
Complete the table, using the labels from the figure. The first label is done for you.
S. No. Description Label a. an angle of reflection on the mirror a b. a partially reflected ray in the glass slab c. a critical angle d. a refracted ray e. an angle of refraction of the ray R For each of the following scenarios, state whether the work done by gravity is positive, negative, or zero.
(a) a person walks on a levelled road.
(b) a person climbs a ladder.
(c) a car in neutral gear is coming down the slope.
The figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
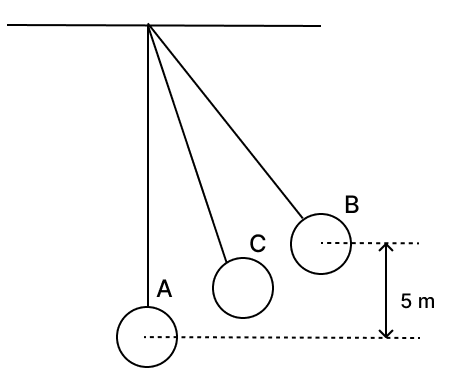
(a) What is the potential energy of the pendulum at the position В?
(b) What is the total mechanical energy at point C?
(c) What is the speed of the bob at the position A when released from B?
(Take g = 10 ms-2 and given that there is no loss of energy.)