Mathematics
The midpoint of the side of a triangle are joined together to get four triangles. These four triangles are:
not equal to each other
congruent to each other
not congruent to each other
none of these
Mid-point Theorem
2 Likes
Answer
From figure,
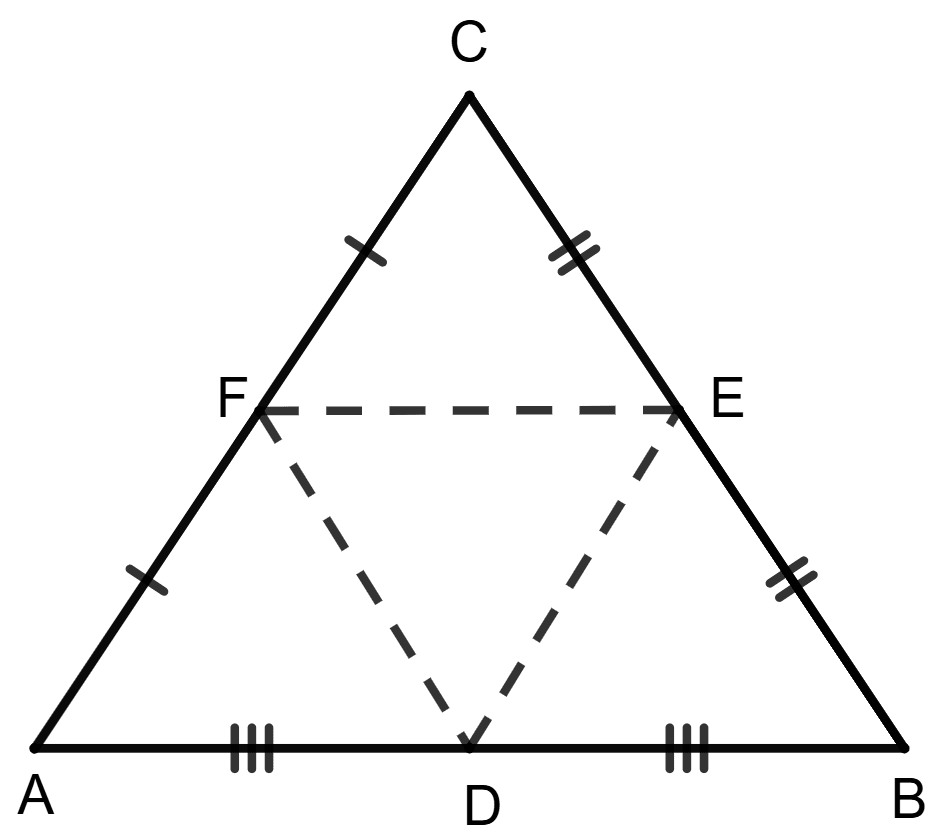
In △ABC,
D, E and F are mid-points of AB, BC and CA respectively.
Now join DE, EF and FD.
To prove :
△ADF ≅ △DBE ≅ △ECF ≅ △DEF
In △ABC,
D and E are midpoints of AB and BC.
∴ DE || AC (By, mid-point theorem) or,
DE || FC ……..(1)
DE || AF ……..(2)
D and F are midpoints of AB and AC.
∴ DF || BC (By, mid-point theorem) or,
DF || EC ……..(3)
DF || BE ……(4)
F and E are midpoints of AC and BC.
∴ FE || AB (By, mid-point theorem) or,
FE || AD ………(5)
FE || DB ………(6)
From (1) and (3) we get,
DE || FC and DF || EC.
Since, opposite sides of a parallelogram are parallel.
∴ DECF is a parallelogram
We know that,
Diagonal of || gm divides it into two congruent triangles.
Diagonal FE divides the parallelogram DECF in two congruent triangles DEF and CEF.
∴ △DEF ≅ △ECF ………(7)
From (2) and (5) we get,
DE || AF and FE || AD.
Since, opposite sides of a parallelogram are parallel.
∴ ADEF is a parallelogram.
We know that,
Diagonal of || gm divides it into two congruent triangles.
Diagonal FD divides the parallelogram in two congruent triangles DEF and AFD.
∴ △DEF ≅ △AFD ………(8)
From (4) and (6) we get,
DF || BE and FE || DB.
∴ DBEF is a parallelogram.
We know that,
Diagonal DE divides the parallelogram in two congruent triangles DEF and DBE.
∴ △DEF ≅ △DBE ………(9)
From equations 7, 8 and 9 we get,
△AFD ≅ △DBE ≅ △ECF ≅ △DEF.
Thus, the four triangles formed are congruent to each other.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
In triangle ABC; M is the mid-point of AB, N is mid-point of AC and D is any point in base BC. Use intercept theorem to show that MN bisects AD.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at right angle.
In the given figure, AB || CD || EF. If AC = 7 cm, AE = 14 cm and BF = 20 cm, then DF is equal to:
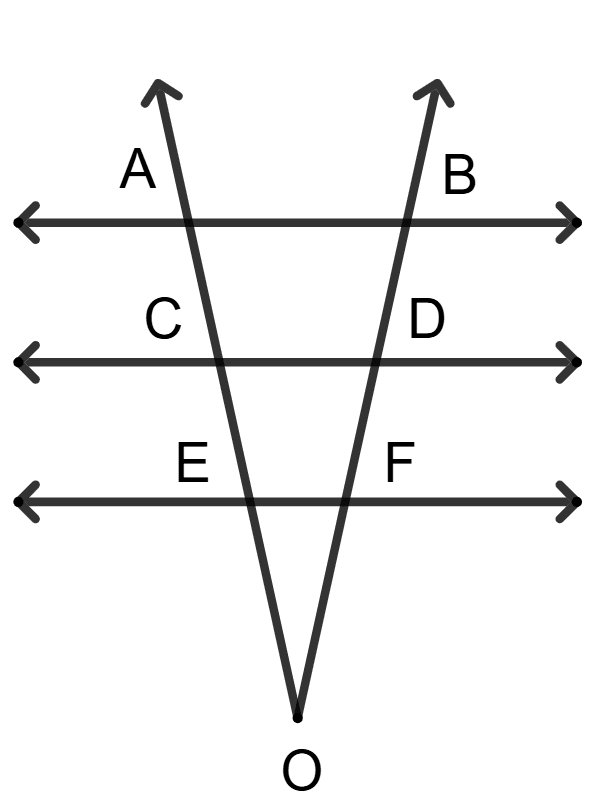
7 cm
14 cm
10 cm
16 cm
In the given figure, AB || CD || EF and E is the mid-point of side AD, then :
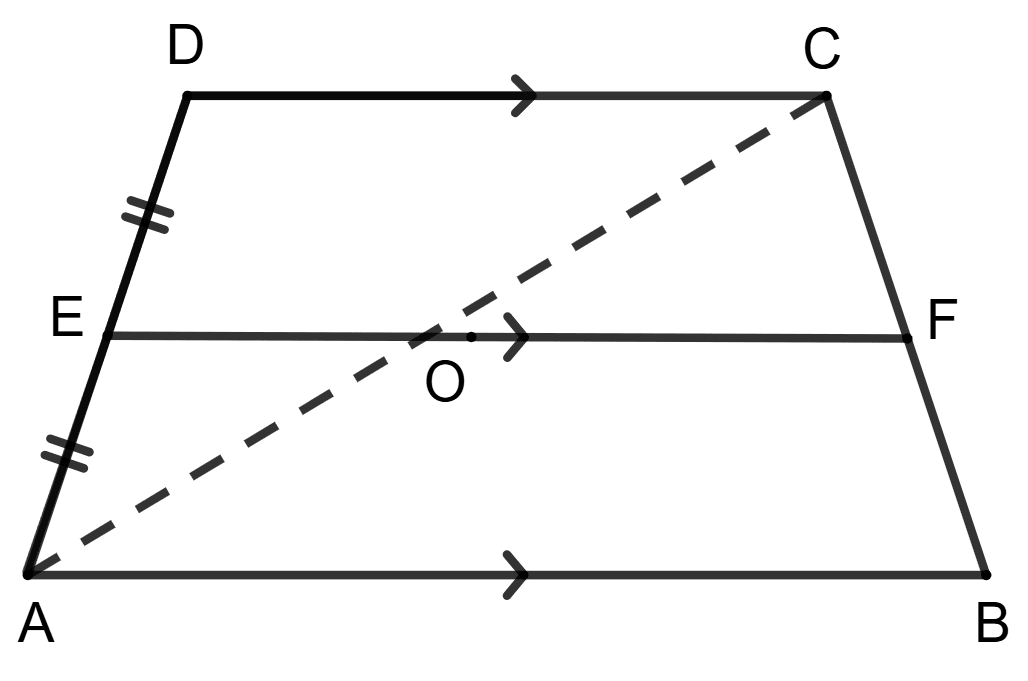
OE : OF = 1 : 3
OE = OF
OF = 2 x OE
CF = FB