Mathematics
Mrs. Rao deposited ₹ 250 per month in a recurring deposit account for a period of 3 years. She received ₹ 10,110 at the time of maturity. Find:
(a) the rate of interest.
(b) how much more interest Mrs. Rao will receive if she had deposited ₹50 more per month at the same rate of interest and for the same time.
GST
27 Likes
Answer
(a) Given,
Mrs. Rao deposited ₹ 250 per month in a recurring deposit account for a period of 3 years.
Total deposit = ₹ 250 × 3 × 12 = ₹ 9,000.
By formula,
Interest = Maturity value - Total deposit = ₹ 10,110 - ₹ 9,000 = ₹ 1,110.
Let rate of interest be r%.
Time (n) = 36 months
By formula,
Substituting values we get :
Hence, rate of interest = 8%.
(b) If per month ₹ 50 more is deposited, then :
P = ₹ 250 + ₹ 50 = ₹ 300.
P = ₹ 300, r = 8%, n = 36 months
By formula,
Substituting values we get :
Additional Interest = New Interest - Old Interest
= ₹1,332 - ₹1,110
= ₹222.
Hence, Mrs. Rao would receive ₹222 more as interest if she had deposited ₹50 more per month at the same rate of interest and for the same time.
Answered By
11 Likes
Related Questions
Assertion (A): The mean of first 9 natural numbers is 4.5.
Statement 2: Mean =
(A) is true, (R) is false.
(A) is false, (R) is true.
Both (A) and (R) are true, and (R) is the correct reason for (A).
Both (A) and (R) are true, and (R) is the incorrect reason for (A).
Solve the following quadratic equation 2x2 − 5x − 4 = 0. Give your answer correct to three significant figures.
In ΔABC, ∠ABC = 90°, AB = 20 cm, AC = 25 cm, DE is perpendicular to AC such that ∠DEA = 90° and DE = 3 cm as shown in the given figure.
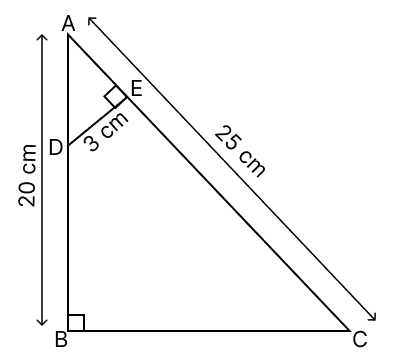
(a) Prove that ΔABC ~ ΔAED.
(b) Find the lengths of BC, AD and AE.
(c) If BCED represents a plot of land on a map whose actual area on ground is 576 m2, then find the scale factor of the map.
Use ruler and compass for the following construction. Construct a ΔABC, where AB = 6 cm, AC = 4.5 cm and ∠BAC = 120°. Construct a circle circumscribing the ΔABC. Measure and write down the length of the radius of the circle.