Mathematics
O is any point inside a rectangle ABCD. Prove that :
OB2 + OD2 = OC2 + OA2.
Pythagoras Theorem
34 Likes
Answer
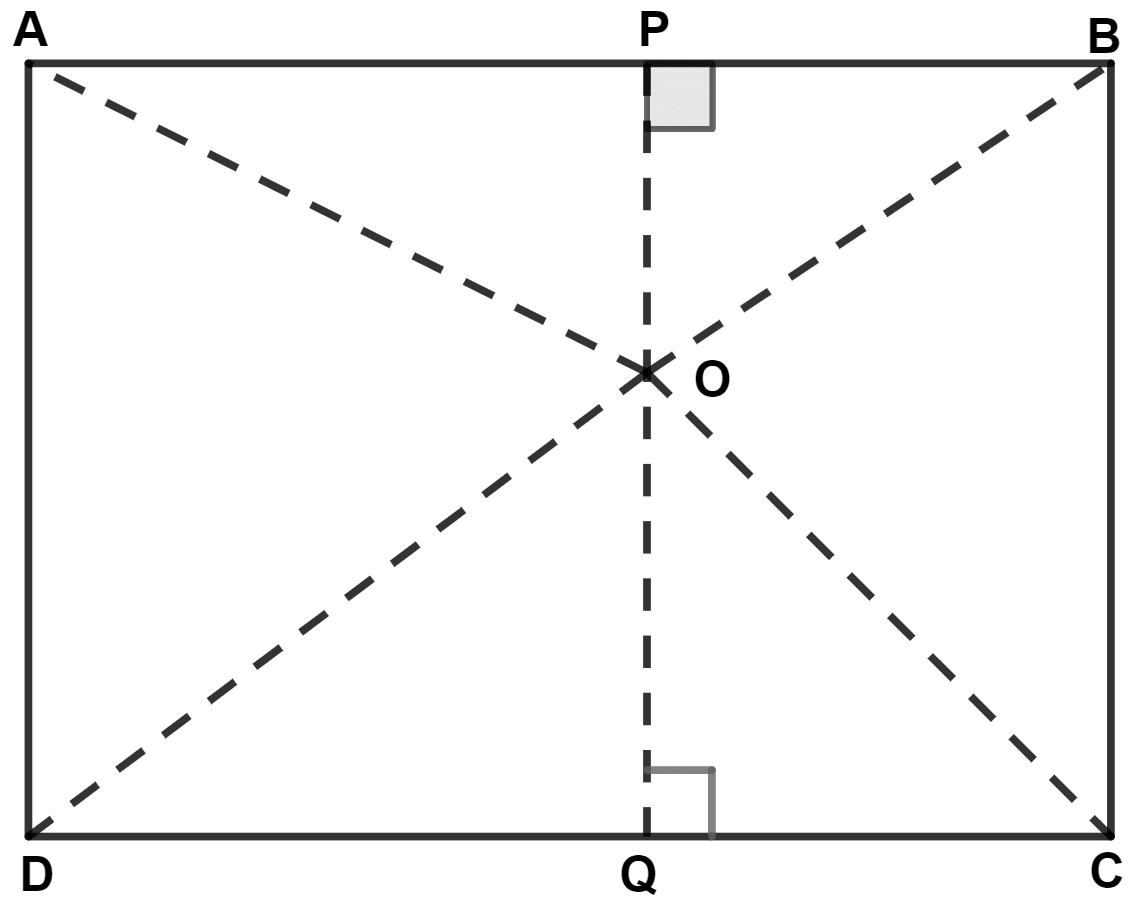
Through point O, draw PQ || BC so that P lies on AB and Q lies on DC.
Since, PQ || BC and AB ⊥ BC,
∴ AB ⊥ PQ and DC ⊥ PQ.
∴ BPQC and APQD are both rectangles.
In right-angled triangle OBP,
By pythagoras theorem,
⇒ OB2 = OP2 + BP2 ……….(1)
In right-angled triangle OQD,
By pythagoras theorem,
⇒ OD2 = OQ2 + DQ2 ……….(2)
In right-angled triangle OQC,
By pythagoras theorem,
⇒ OC2 = OQ2 + QC2 ……….(3)
In right-angled triangle OAP,
By pythagoras theorem,
⇒ OA2 = OP2 + AP2 ……….(4)
Adding equations (1) and (2), we get :
⇒ OB2 + OD2 = OP2 + BP2 + OQ2 + DQ2
= OP2 + CQ2 + OQ2 + AP2 (As, BP = CQ and DQ = AP)
= CQ2 + OQ2 + OP2 + AP2
= OC2 + OA2. [From equation (3) and (4)]
Hence, proved that OB2 + OD2 = OC2 + OA2.
Answered By
21 Likes
Related Questions
In a rectangle ABCD, prove that :
AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°. Prove that :
2AC2 - AB2 = BC2 + CD2 + DA2.
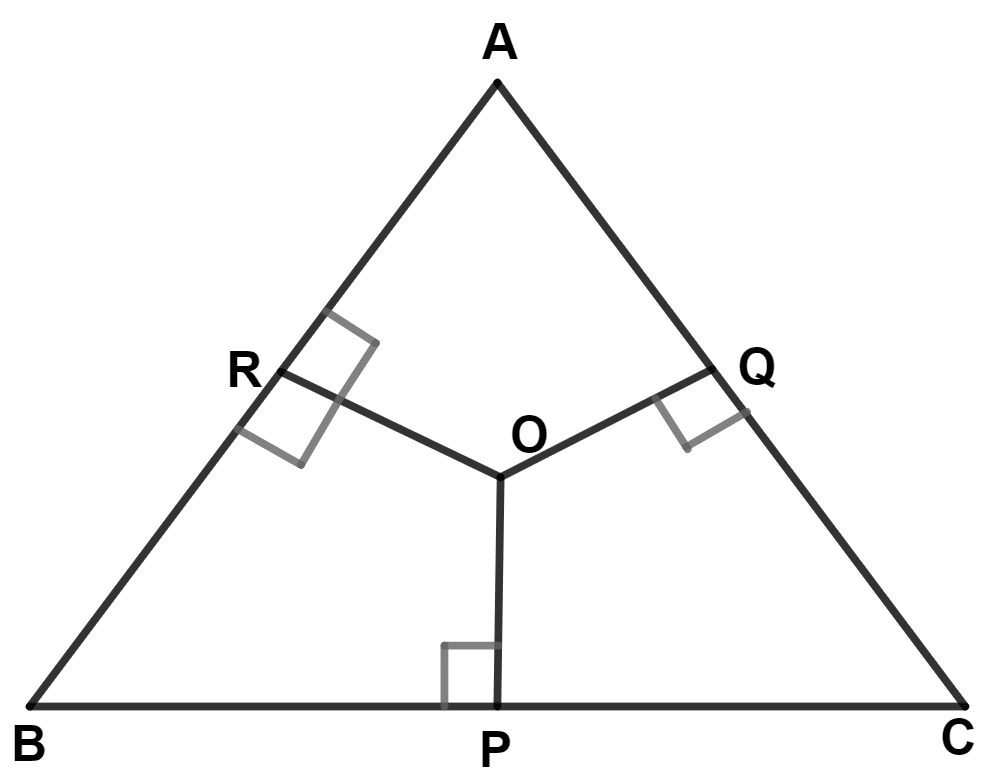
In the following figure, OP, OQ and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC. Prove that :
AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2.
Angle AOB is:
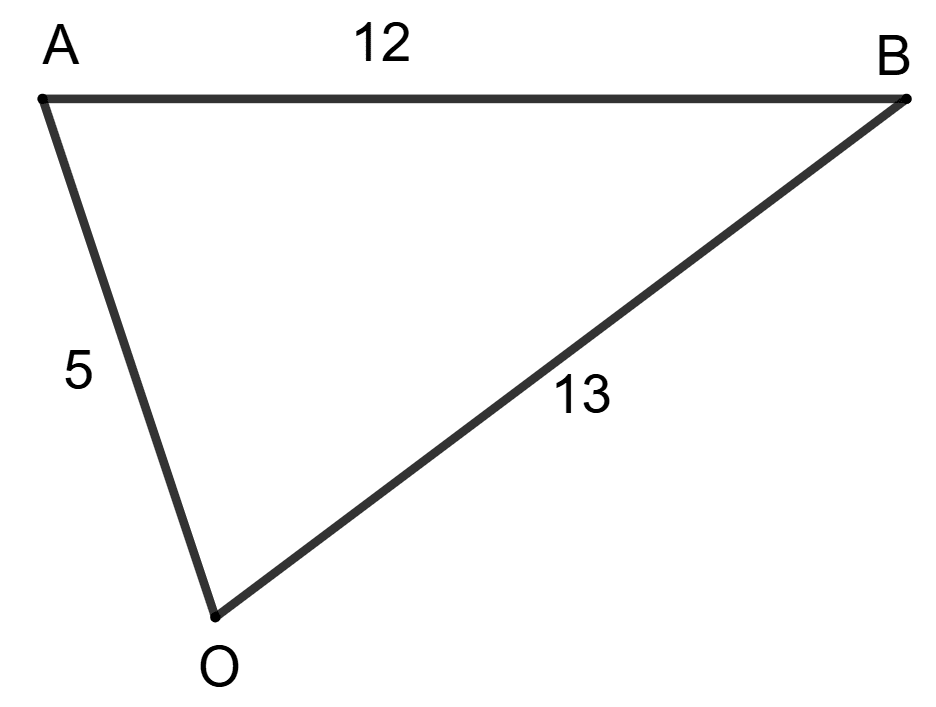
60°
90°
45°
none of these