Physics
An object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
(a) What is the nature of the image so formed?
(b) Calculate the distance of the image from the lens.
Refraction Lens
4 Likes
Answer
(a) As, the object distance (= 24 cm) is greater than the focal length (= 8 cm) of the convex lens which means the object placed beyond it's focus so the lens will form a real and inverted image.
(b)
Given,
Object distance (u) = - 24 cm
Focal length (f) = +8 cm
From lens formula,
∴ The image is formed at a distance of 12 cm behind the lens.
Answered By
2 Likes
Related Questions
The refractive index of water is 1.33 at a certain temperature. When the temperature of water is increased by 40°C, the refractive index changes to 'x'.
(a) State whether x < 1.33 or x > 1.33.
(b) State two differences between normal reflection and total internal reflection.
(a) Mixture of red + blue + green is passed through a convex lens as shown in the diagram below. State whether the ray passes through a single point or through different points on the principal axis after refraction.
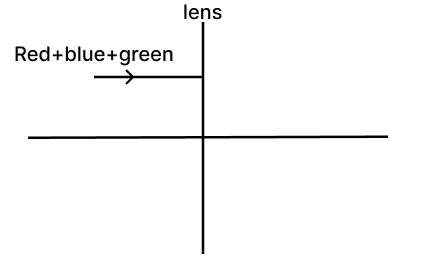
(b) Name the invisible radiations which are studied using the quartz prism.
(c) State one use of these radiations.
(d) Name one radiation having the wavelength longer than the wavelength of these radiations.
When sunlight passes through water droplets in the atmosphere it gets dispersed into its constituent colours forming a rainbow. A similar phenomenon is observed when white light passes through a prism.
(a) Which colour will show the maximum angle of deviation and which colour will show the minimum angle of deviation?
(b) If Instead of sunlight, a green-coloured ray is passed through a glass prism. What will be the colour of the emergent ray?
O is a luminescent particle trapped inside a glass block. A student traces the path of rays coming out of it and reflecting over a plane mirror as shown in the diagram below.
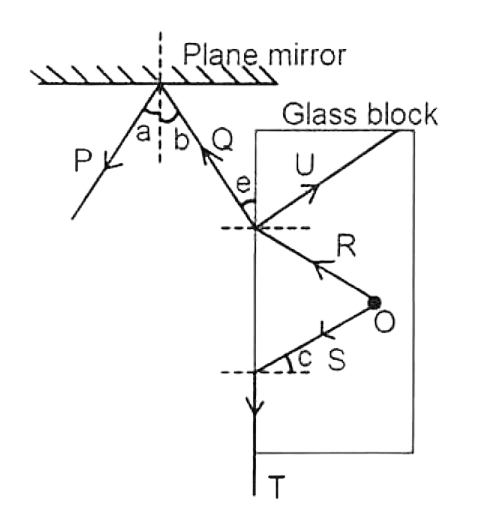
Complete the table, using the labels from the figure. The first label is done for you.
S. No. Description Label a. an angle of reflection on the mirror a b. a partially reflected ray in the glass slab c. a critical angle d. a refracted ray e. an angle of refraction of the ray R