Mathematics
In parallelogram ABCD, diagonal AC and BD intersect each other at point O. Then:
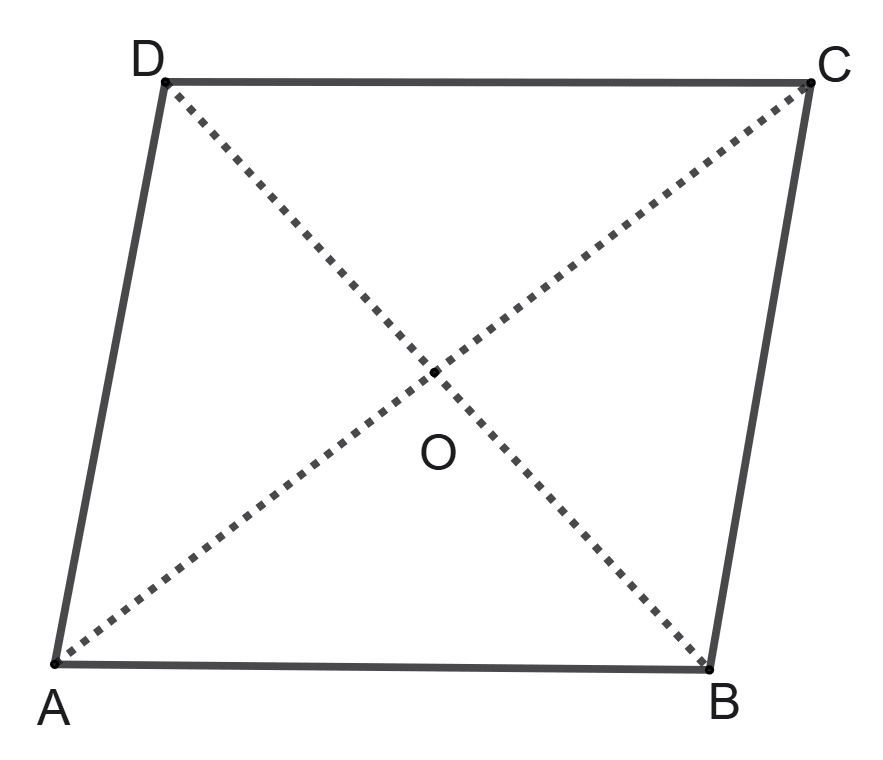
AC = BD
∠AOB = 90°
The four triangles formed are congruent
AC and BD bisect each other
Rectilinear Figures
4 Likes
Answer
Given; ABCD is a parallelogram in which AC and BD are the diagonals of the parallelogram.
As we know that in a parallelogram, opposite sides are parallel and equal in length, opposite angles are equal and consecutive angles are supplementary.
Option 1: AC = BD is true only for rectangles or squares, not all parallelograms.
Option 2: ∠AOB = 90° is true only for rhombuses or squares, not all parallelograms.
Option 3: The four triangles formed are congruent is true only for rhombuses or squares, not all parallelograms.
Option 4: AC and BD bisect each other is a fundamental property of all parallelograms.
Hence, option 4 is the correct option.
Answered By
3 Likes
Related Questions
At a vertex of a regular polygon, exterior angle is 120°. Then the number of sides of this polygon is:
3
4
5
6
A quadrilateral ABCD is a trapezium if:
AB = DC
AD = BC
∠A + ∠C = 180°
∠B + ∠C = 180°
Statement 1: The sum of the interior angles of a regular polygon is twice of the sum of its exterior angles.
Statement 2: Number of sides(n) of the polygon is 6.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: Through a vertex of a polygon, 3 diagonals can be drawn.
Statement 2: The polygon is hexagon.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.