Mathematics
The perimeter of a rhombus is 96 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.
Trigonometric Identities
5 Likes
Answer
ABCD is a rhombus.
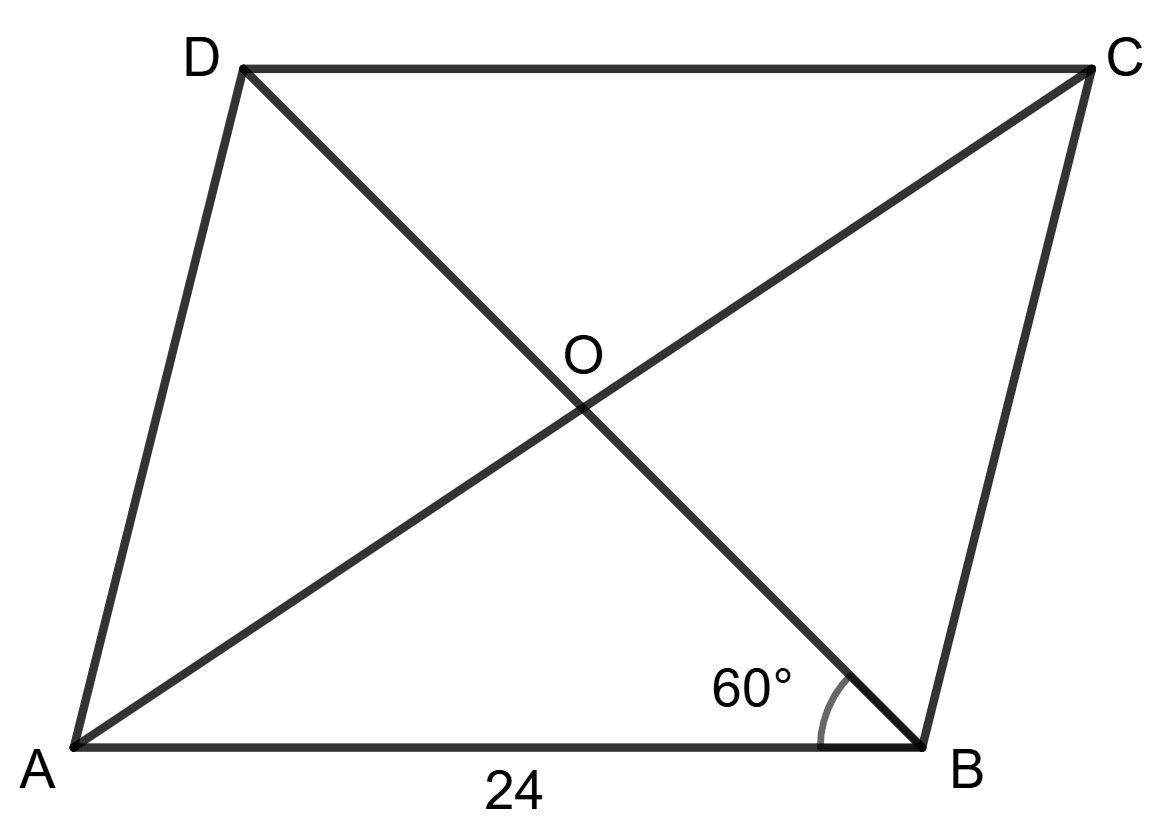
Perimeter of rhombus = 4 x side
Hence, side AB = BC = CD = DA = = 24 cm
∠ ABC = 120°
As we know that diagonal of a rhombus bisect each other at 90°.
In Δ ABO,
∠ ABO = = 60°
∴ AC = 2 x AO = 2 x 20.78 = 41.56 cm
Similarly,
∴ BD = 2 x BO = 2 x 12 = 24 cm
Hence, the lengths of the diagonals are: AC = 41.56 cm and BD = 24 cm.
Answered By
3 Likes