Mathematics
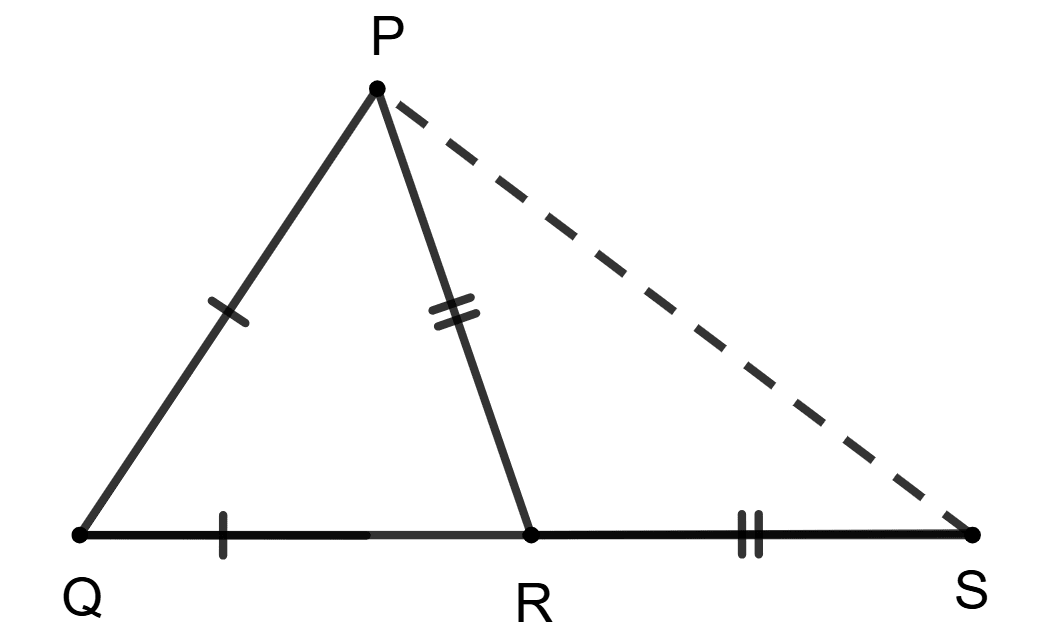
ΔPQR is an isosceles triangle such that PQ = QR. If S is a point on QR produced such that PR = RS and ∠QPS = 63°, find ∠PSQ.
Triangles
24 Likes
Answer
ΔPQR is an isosceles triangle such that PQ = QR.
S is a point on QR produced such that PR = RS.
As we know that in an isosceles triangle, angles opposite to equal sides are equal.
In ΔPQR,
⇒ ∠QPR = ∠QRP = x° (let)………………..(1)
In ΔPRS,
⇒ ∠PSR = ∠SPR = y° (let)………………..(2)
Given,
⇒ ∠QPS = 63°
From figure,
⇒ ∠QPR + ∠SPR = 63°
⇒ x° + y° = 63° ………………(3)
We know that,
The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
The angle ∠PRQ (which is x) is an exterior angle to △PRS at vertex R.
⇒ ∠PRQ = ∠SPR + ∠PSR.
⇒ x° = y° + y°
⇒ x° = 2y°
Substituting the above value of x in equation (1), we get :
⇒ 2y° + y° = 63°
⇒ 3y° = 63°
⇒ y° =
⇒ y° = 21°
⇒ ∠PSR = ∠SPR = 21°.
From figure,
⇒ ∠PSQ = ∠PSR = 21°
Hence, ∠PSQ = 21°.
Answered By
17 Likes
Related Questions
In a triangle ABC, AB = AC, D and E are points on the sides AB and AC respectively such that BD = CE. Show that:
(i) △DBC ≅ △ECB
(ii) ∠DCB = ∠EBC
(iii) OB = OC, where O is the point of intersection of BE and CD.
ABC is an isosceles triangle in which AB = AC. P is any point in the interior of △ABC such that ∠ABP = ∠ACP. Prove that
(a) BP = CP
(b) AP bisects ∠BAC.
In the adjoining figure, D and E are points on the side BC of △ABC such that BD = EC and AD = AE. Show that △ABD ≅ △ACE.

In the figure (i) given below, CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that △ADE ≅ △BCE and hence, AEB is an isosceles triangle.